
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.
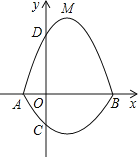
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求![]() 的值.
的值.
【答案】解:(1)令y=0,则 ![]() ,
,
∵m<0,∴![]() ,解得:
,解得:![]() ,
, ![]() 。
。
∴A(![]() ,0)、B(3,0)。
,0)、B(3,0)。
(2)存在。理由如下:
∵设抛物线C1的表达式为![]() (
(![]() ),
),
把C(0,![]() )代入可得,
)代入可得,![]() 。
。
∴C1的表达式为:![]() ,即
,即![]() 。
。
设P(p,![]() ),
),
∴ S△PBC = S△POC + S△BOP –S△BOC =![]() 。
。
∵![]() <0,∴当
<0,∴当![]() 时,
时,![]() S△PBC最大值为
S△PBC最大值为![]() 。
。
(3)由C2可知: B(3,0),D(0,![]() ),M(1,
),M(1,![]() ),
),
∴BD2=![]() ,BM2=
,BM2=![]() ,DM2=
,DM2=![]() 。
。
∵∠MBD<90°, ∴讨论∠BMD=90°和∠BDM=90°两种情况:
当∠BMD=90°时,BM2+ DM2= BD2 ,即![]() +
+![]() =
=![]() ,
,
解得:![]() ,
, ![]() (舍去)。
(舍去)。
当∠BDM=90°时,BD2+ DM2= BM2 ,即![]() +
+![]() =
=![]() ,
,
解得:![]() ,
,![]() (舍去) 。
(舍去) 。
综上所述, ![]() 或
或![]() 时,△BDM为直角三角形。
时,△BDM为直角三角形。
【解析】(1)在![]() 中令y=0,即可得到A、B两点的坐标。
中令y=0,即可得到A、B两点的坐标。
(2)先用待定系数法得到抛物线C1的解析式,由S△PBC = S△POC + S△BOP –S△BOC得到△PBC面积的表达式,根据二次函数最值原理求出最大值。
(3)先表示出DM2,BD2,MB2,再分两种情况:①∠BMD=90°时;②∠BDM=90°时,讨论即可求得m的值。


科目:初中数学 来源: 题型:
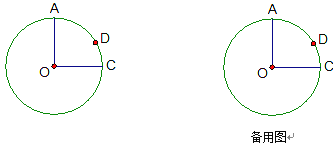
【题目】如图,⊙O的半径OA⊥OC,点D在![]() 上,且
上,且![]() =2
=2![]() ,OA=4.
,OA=4.
(1)∠COD= °;
(2)求弦AD的长;
(3)P是半径OC上一动点,连结AP、PD,请求出AP+PD的最小值,并说明理由.
(解答上面各题时,请按题意,自行补足图形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(P点与A、B两点不重合).如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
(1)直接写出抛物线y=-x2+1的勾股点的坐标.
(2)如图②,已知抛物线y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1, ![]() )是抛物线的勾股点,求抛物线的函数表达式.
)是抛物线的勾股点,求抛物线的函数表达式.
(3)在(2)的条件下,点Q在抛物线上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
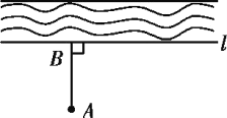
【题目】(1)如图,要把小河里的水引到田地A处,就作AB⊥l(垂足为B),沿AB挖水沟,水沟最短.理由是___________.
(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式._____________________________ .
(3)比较大小:![]() ______
______ ![]() .
.
(4)已知![]() 与
与![]() 是同类项,则m-3n的平方根是___.
是同类项,则m-3n的平方根是___.
(5)已知点P的坐标为(3a+6,2﹣a),且点P到两坐标轴的距离相等,则点P的坐标是______.
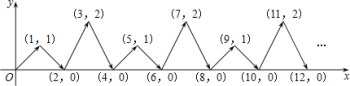
(6) 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是______________
查看答案和解析>>
科目:初中数学 来源: 题型:
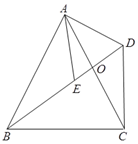
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两段材料,回答下列各题:
材料一:规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如:![]() ,
,![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“2的圈3次方”,
,读作“2的圈3次方”,![]() 记作
记作![]() ,读作“
,读作“![]() 的圈4次方”,一般地,把
的圈4次方”,一般地,把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”.
次方”.
材料二:求值:![]() . 解:设
. 解:设![]() ,将等式两边同时乘以2得:
,将等式两边同时乘以2得:![]() 将下式减去上式得
将下式减去上式得![]() 即
即![]()
(1)直接写出计算结果:![]()
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?试一试:将下列运算结果直接写成幂的形式:![]() (
(![]() 且
且![]() 为正整数)
为正整数)
(3)计算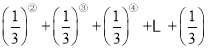
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c+1。
(1)当b=1时,求这个二次函数的对称轴的方程;
(2)若c=﹣![]() b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
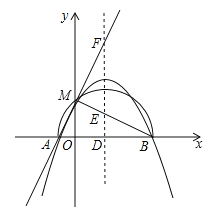
(3)若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,b>0,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足![]() =
=![]() ,求二次函数的表达式.
,求二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度![]() 与甲盒数量
与甲盒数量![]() 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com