
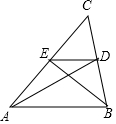
 如图,AD、BE是△ABC的两条中线,△EDC的面积是2,则△ABD的面积是4.
如图,AD、BE是△ABC的两条中线,△EDC的面积是2,则△ABD的面积是4.  同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:填空题
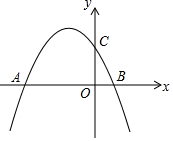 如图,二次函数Y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是8.
如图,二次函数Y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x2-15x+20 | B. | 3x2-9x+8 | C. | 3x2-6x-20 | D. | 3x2-12x-9 |
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
某工厂现在平均每天比原计划多生产50台机器,现在生产800台所需时间与原计划生产600台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )
A. 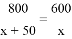 B.
B. 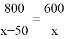 C.
C.  D.
D. 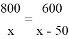
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com