
【题目】如图,点![]() 都在反比例函数
都在反比例函数![]() 的图象上.
的图象上.
(1)求![]() 的值;
的值;
(2)如果![]() 为
为![]() 轴上一点,
轴上一点,![]() 为
为![]() 轴上一点,以点
轴上一点,以点![]() 为顶点的四边形是平行四边形,试求直线
为顶点的四边形是平行四边形,试求直线![]() 的函数表达式;
的函数表达式;
(3)将线段![]() 沿直线
沿直线![]() 进行对折得到线段
进行对折得到线段![]() ,且点
,且点![]() 始终在直线
始终在直线![]() 上,当线段
上,当线段![]() 与
与![]() 轴有交点时,则
轴有交点时,则![]() 的取值范围为_______(直接写出答案)
的取值范围为_______(直接写出答案)

【答案】(1)m=3,k=12;(2)y![]() x+2或y
x+2或y![]() x﹣2;(3)
x﹣2;(3)![]() .
.
【解析】
(1)由题可得m(m+1)=(m+3)(m﹣1)=k,解这个方程就可求出m、k的值.
(2)由于点A、点B是定点,可对线段AB进行分类讨论:AB是平行四边形的边、AB是平行四边形的对角线,再利用平行四边形的性质、中点坐标公式及直线的相关知识就可解决问题.
(3)由于点A关于直线y=kx+b的对称点点A1始终在直线OA上,因此直线y=kx+b必与直线OA垂直,只需考虑两个临界位置(A1在x轴上、B1在x轴上)对应的b的值,就可以求出b的取值范围.
(1)∵点A(m,m+1),B(m+3,m﹣1)都在反比例函数y![]() 的图象上,∴m(m+1)=(m+3)(m﹣1)=k.
的图象上,∴m(m+1)=(m+3)(m﹣1)=k.
解得:m=3,k=12,∴m、k的值分别为3、12.
(2)设点M的坐标为(m,0),点N的坐标为(O,n).
①若AB为平行四边形的一边.
Ⅰ.点M在x轴的正半轴,点N在y轴的正半轴,连接BN、AM交于点E,连接AN、BM,如图1.
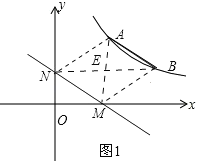
∵四边形ABMN是平行四边形,∴AE=ME,NE=BE.
∵A(3,4)、B(6,2)、M(m,0)、N(0,n),∴由中点坐标公式可得:
xE![]() ,yE
,yE![]() ,∴m=3,n=2,∴M(3,0)、N(0,2).
,∴m=3,n=2,∴M(3,0)、N(0,2).
设直线MN的解析式为y=kx+b.
则有![]()
解得: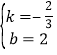 ,∴直线MN的解析式为y
,∴直线MN的解析式为y![]() x+2.
x+2.
Ⅱ.点M在x轴的负半轴,点N在y轴的负半轴,连接BM、AN交于点E,连接AM、BN,如图2,同理可得:直线MN的解析式为y![]() x﹣2.
x﹣2.
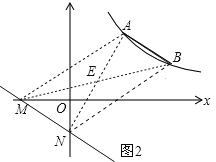
②若AB为平行四边形的一条对角线,连接AN、BM,设AB与MN交于点F,如图3.
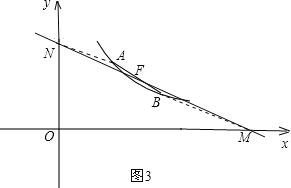
同理可得:直线MN的解析式为y![]() x+6,此时点A、B都在直线MN上,故舍去.
x+6,此时点A、B都在直线MN上,故舍去.
综上所述:直线MN的解析式为y![]() x+2或y
x+2或y![]() x﹣2.
x﹣2.
(3)①当点B1落到x轴上时,如图4.
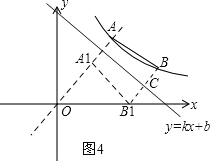
设直线OA的解析式为y=ax.
∵点A的坐标为(3,4),∴3a=4,即a![]() ,∴直线OA的解析式为y
,∴直线OA的解析式为y![]() x.
x.
∵点A1始终在直线OA上,∴直线y=kx+b与直线OA垂直,∴![]() k=﹣1,∴k
k=﹣1,∴k![]() .
.
由于BB1∥OA,因此直线BB1可设为y![]() x+c.
x+c.
∵点B的坐标为(6,2),∴![]() 6+c=2,即c=﹣6,∴直线BB1解析式为y
6+c=2,即c=﹣6,∴直线BB1解析式为y![]() x﹣6.
x﹣6.
当y=0时,![]() x﹣6=0.则有x
x﹣6=0.则有x![]() ,∴点B1的坐标为(
,∴点B1的坐标为(![]() ,0).
,0).
∵点C是BB1的中点,∴点C的坐标为(![]() )即(
)即(![]() ,1).
,1).
∵点C在直线y![]() x+b上,∴
x+b上,∴![]() b=1.
b=1.
解得:b![]() .
.
②当点A1落到x轴上时,如图5.
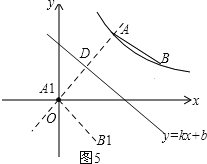
此时,点A1与点O重合.
∵点D是AA1的中点,A(3,4),A1(0,0),∴D(![]() ,2).
,2).
∵点D在直线y![]() x+b上,∴
x+b上,∴![]() b=2.
b=2.
解得:b![]() .
.
综上所述:当线段A1B1与x轴有交点时,则b的取值范围为![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,绘出了某一结果出现的频率的折线图,则符合这一结果的实验可能是
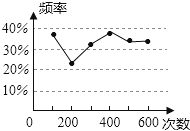
A. 掷一枚正六面体的骰子,出现1点的概率
B. 抛一枚硬币,出现正面的概率
C. 任意写一个整数,它能被2整除的概率
D. 从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资![]() (吨)与时间
(吨)与时间![]() (小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
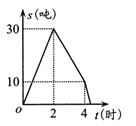
A. 4小时B. 4.3小时C. 4.4小时D. 5小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 过点
过点![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() ,作
,作![]() 轴于点
轴于点![]() .设点
.设点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() .
.

(1)填空:![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)探究:是否存在这样的点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)设![]() 的周长为
的周长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )

A. 8B. 10C. 10.4D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为( )
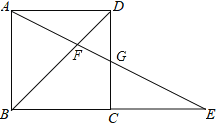
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )

A. 10B. 4![]() C. 20D. 8
C. 20D. 8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
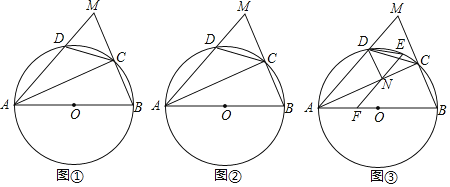
【题目】已知:在![]() 中,C、D分别为BM、AM上的点,四边形ABCD内接于
中,C、D分别为BM、AM上的点,四边形ABCD内接于![]() ,连接AC,
,连接AC,![]() ;
;
![]() 如图
如图![]() ,求证:弧
,求证:弧![]() 弧BD;
弧BD;
![]() 如图
如图![]() ,若AB为直径,
,若AB为直径,![]() ,求
,求![]() 值;
值;
![]() 如图
如图![]() ,在
,在![]() 的条件下,E为弧CD上一点
的条件下,E为弧CD上一点![]() 不与C、D重合
不与C、D重合![]() ,F为AB上一点,连接EF交AC于点N,连接DN、DE,若
,F为AB上一点,连接EF交AC于点N,连接DN、DE,若![]() ,
,![]() ,
,![]() ,求AN的长.
,求AN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com