
 如图,在平面直角坐标系中,抛物线y=$\frac{1}{5}$x2+bx+c经过点A(-5,2)、B(5,12).
如图,在平面直角坐标系中,抛物线y=$\frac{1}{5}$x2+bx+c经过点A(-5,2)、B(5,12).分析 (1)利用待定系数法求出抛物线的函数表达式;
(2)如图1中,设线段BO与抛物线交于点F,当点C与点F重合时,CM=MN,列方程组即可解决问题.
(3)①如图2中,作EN⊥x轴于N,NE的延长线交BD于M,求出PM、ME即可解决问题.
②点F在点B的左右两侧均有可能,需要分类讨论.综合利用相似三角形的性质、等腰三角形的性质和勾股定理,求出线段BM的长度.
解答 解:(1)∵抛物线y=$\frac{1}{5}$x2+bx+c经过点A(-5,2)、B(5,12),
∴$\left\{\begin{array}{l}{5-5b+c=2}\\{5+5b+c=12}\end{array}\right.$解得$\left\{\begin{array}{l}{b=1}\\{c=2}\end{array}\right.$,
∴抛物线解析式为y=$\frac{1}{5}$x2+x+2.
(2)如图1中,设线段BO与抛物线交于点F,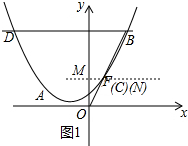
①当点C与点F或B重合时,CM=MN,
∵直线OB解析式为y=$\frac{12}{5}$x,
由$\left\{\begin{array}{l}{y=\frac{12}{5}x}\\{y=\frac{1}{5}{x}^{2}+x+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=5}\\{y=12}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=\frac{24}{5}}\end{array}\right.$,
∴点C坐标(2,$\frac{24}{5}$)或(5,12),
∴点C横坐标为2或5.
②当点N在y轴左侧时,设C(m,$\frac{12}{5}m$),
∵MN=CM,
∴$\frac{1}{5}$m2-m+2=$\frac{12}{5}$m,
∴m=$\frac{17-\sqrt{149}}{2}$或$\frac{17+\sqrt{149}}{2}$(不合题意舍弃),
综上所述,点C的横坐标为2或5或$\frac{17-\sqrt{149}}{2}$.
(3)①如图2中,作EN⊥x轴于N,NE的延长线交BD于M.
∵点E坐标($\frac{5}{2}$,6),
∴BM=$\frac{5}{2}$,EN=6,EM=6,
∵抛物线对称轴x=-$\frac{5}{2}$,
∴PB=$\frac{15}{2}$,PM=PB-BM=5,
在Rt△PME中,tan∠BPE=$\frac{EM}{PM}$=$\frac{6}{5}$.
②如图3中,当点F在点B左侧时,BD与y轴交于点K,连接KE.
∵OE=EB,
∴KE=EO=EB,
∵∠FEO=3∠BFE,∠FEO=∠BFE+∠FBE,
∴∠FBE=2∠BFE=∠BEE,
∵∠BKE=∠BFE+∠KEF,
∴∠KFE=∠KEF,
∴FK=KE=$\frac{1}{2}$OB=$\frac{13}{2}$,
∴BF=KF+BK=$\frac{13}{2}$+5=$\frac{23}{2}$,
当点F′在点B右侧时,在BD上截取BG=BE,作EN⊥BD于N.
∵∠F′EO=3∠EF′B,∠F′EO=∠EF′B+∠EBF′,
∴∠EBF′=2∠EF′B,
∵∠BGE=∠BEG,
∴∠BEG=∠EF′B,∵∠EGB=∠EGF′,
∴△BGE∽△EGF′,
∴$\frac{GF′}{GE}$=$\frac{GE}{GB}$,
在Rt△ENG中,∵NE=6,GN=4,
∴GE=$\sqrt{G{N}^{2}+N{E}^{2}}$=2$\sqrt{13}$,设BF′=x,
∴$\frac{\frac{13}{2}+x}{2\sqrt{13}}$=$\frac{2\sqrt{13}}{\frac{13}{2}}$,
∴x=$\frac{3}{2}$,
综上所述当∠BFE=$\frac{1}{3}$∠FEO时,请直接写出线段BF的长为$\frac{23}{2}$或$\frac{3}{2}$.
点评 本题是中考压轴题,考查了二次函数的图象与性质、待定系数法、解方程、相似三角形、等腰三角形、平行四边形、勾股定理等知识点.难点在于第(3)②问,满足条件的点F可能有两种情形,需要分类讨论,分别计算,避免漏解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
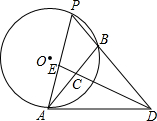 如图,AD切⊙O于A,DBP交⊙O于B,P,C为AB的中点,DC的延长线交AB于E,求证:$\frac{B{D}^{2}}{A{D}^{2}}$=$\frac{AE}{EP}$.
如图,AD切⊙O于A,DBP交⊙O于B,P,C为AB的中点,DC的延长线交AB于E,求证:$\frac{B{D}^{2}}{A{D}^{2}}$=$\frac{AE}{EP}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某批发商批发某种商品的单价P(单位:元/kg)与一次性批发数量Q(单位:kg)之间函数的图象如图所示,一零售商仅有现金2700元,他最多可购买这种商品90kg(不考虑运输费等其他费用).
某批发商批发某种商品的单价P(单位:元/kg)与一次性批发数量Q(单位:kg)之间函数的图象如图所示,一零售商仅有现金2700元,他最多可购买这种商品90kg(不考虑运输费等其他费用).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com