

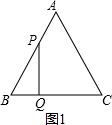
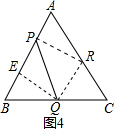
 为何值时,△BPQ为直角三角形;
为何值时,△BPQ为直角三角形; 的函数关系式;
的函数关系式; 为何值时,△APR∽△PRQ ?
为何值时,△APR∽△PRQ ?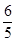 或3;(2)
或3;(2)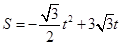 ;(3)
;(3)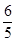 .
.
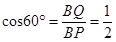
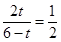 ,
,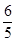 (秒);
(秒);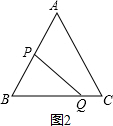
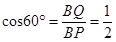 ,即
,即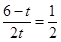 ,
,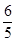 或3时,△BPQ为直角三解形;
或3时,△BPQ为直角三解形;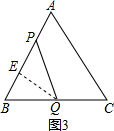
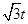
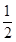 ×BP×QE=
×BP×QE=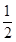 (6-t)×
(6-t)×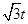 =
=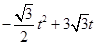
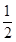 ×2t=t,
×2t=t,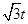
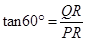 ,即
,即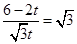 ,
,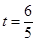 ,
,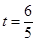 时,△APR∽△PRQ.
时,△APR∽△PRQ.

 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源:不详 题型:解答题
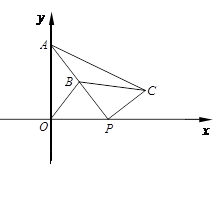
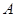 的坐标为
的坐标为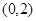 ,点
,点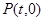 在
在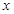 轴上,
轴上,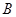 是线段
是线段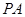 的中点.将线段
的中点.将线段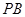 绕着点
绕着点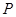 顺时针方向旋转
顺时针方向旋转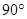 ,得到线段
,得到线段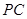 ,连结
,连结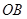 、
、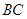 .
.
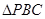 的形状,并简要说明理由;
的形状,并简要说明理由;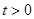 时,试问:以
时,试问:以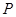 、
、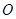 、
、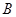 、
、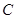 为顶点的四边形能否为平行四边形?若能,求出相应的
为顶点的四边形能否为平行四边形?若能,求出相应的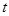 的值?若不能,请说明理由;
的值?若不能,请说明理由;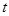 为何值时,
为何值时,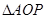 与
与 相似?
相似?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.AB∥EF |
| B.AB+DC=2EF |
| C.四边形AEFB和四边形ABCD相似. |
| D.EG=FH |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A. | B.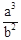 | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com