
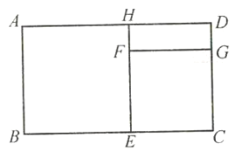
【题目】如图,长方形![]() 中,长
中,长![]() ,宽
,宽![]() ,四边形
,四边形![]() 和四边形
和四边形![]() 都是正方形.
都是正方形.
(1)求四边形![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)当![]() 、
、![]() 满足什么等量关系时,图形是一个轴对称图形.
满足什么等量关系时,图形是一个轴对称图形.
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
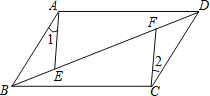
【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
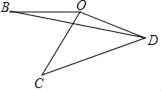
【题目】将线段OB绕点O逆时针旋转60°得到线段OC,继续旋转α(0°<α<120°)得到线段OD,连接CD.
(1)如图,连接BD,则∠BDC的大小=_____(度);
(2)将线段OB放在平面直角坐标系中,O是坐标原点,点B的坐标为(﹣6,0),以OB为斜边作Rt△OBE,使∠OBE=∠OCD,且点E在第三象限,若∠CED=90°,则α的大小=_____(度),点D的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
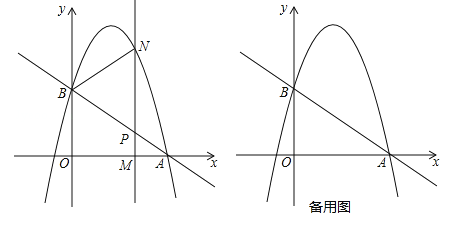
【题目】如图,抛物线y=﹣![]() +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)在对称轴的左侧是否存在点M使四边形OMPB的面积最大,如果存在求点M的坐标;不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
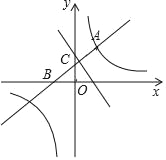
【题目】如图,直线y=x+b与双曲线y=![]() (k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.
(k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.
(1)求直线和双曲线的解析式;
(2)若△BCP的面积等于2,求P点的坐标;
(3)求PA+PC的最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com