
【题目】如图,在平面直角坐标系中,己知点![]() ,点
,点![]() 在
在![]() 轴上,并且
轴上,并且![]() ,动点
,动点![]() 在过
在过![]() 三点的拋物线上.
三点的拋物线上.

(1)求抛物线的解析式.
(2)作垂直![]() 轴的直线,在第一象限交直线
轴的直线,在第一象限交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,求当线段
,求当线段![]() 的长有最大值时
的长有最大值时![]() 的坐标.并求出
的坐标.并求出![]() 最大值是多少.
最大值是多少.
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得△
,使得△![]() 是等腰三角形?若存在,请直接写出点
是等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 最大值为4,此时
最大值为4,此时![]() 的坐标为
的坐标为![]() ;(3)存在,
;(3)存在,![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)先确定A(4,0),B(-1,0),再设交点式y=a(x+1)(x-4),然后把C点坐标代入求出a即可;
(2)作PE⊥x轴,交AC于D,垂足为E,如图,易得直线AC的解析式为y=-x+4,设P(x,-x2+3x+4)(0<x<4),则D(x,-x+4),再用x表示出PD,然后根据二次函数的性质解决问题;
(3)先计算出AC=4![]() ,再分类讨论:当QA=QC时,易得Q(0,0);当CQ=CA时,利用点Q与点A关于y轴对称得到Q点坐标;当AQ=AC=4
,再分类讨论:当QA=QC时,易得Q(0,0);当CQ=CA时,利用点Q与点A关于y轴对称得到Q点坐标;当AQ=AC=4![]() 时可直接写出Q点的坐标.
时可直接写出Q点的坐标.
(1)∵C(0,4),
∴OC=4,
∵OA=OC=4OB,
∴OA=4,OB=1,
∴A(4,0),B(-1,0),
设抛物线解析式为y=a(x+1)(x-4),
把C(0,4)代入得a×1×(-4)=4,解得a=-1,
∴抛物线解析式为y=-(x+1)(x-4),
即y=-x2+3x+4;
(2)作PE⊥x轴,交AC于D,垂足为E,如图,

设直线AC的解析式为:y=kx+b,
∵A(4,0),C(0,4)
∴![]()
解得,![]()
∴直线AC的解析式为y=-x+4,
设P(x,-x2+3x+4)(0<x<4),则D(x,-x+4),
∴PD=-x2+3x+4-(-x+4)=-x2+4x=-(x-2)2+4,
当x=2时,PD有最大值,最大值为4,此时P点坐标为(2,6);
(3)存在.
∵OA=OC=4,
∴AC=4![]() ,
,
∴当QA=QC时,Q点在原点,即Q(0,0);
当CQ=CA时,点Q与点A关于y轴对称,则Q(-4,0);
当AQ=AC=4![]() 时,Q点的坐标(4+4
时,Q点的坐标(4+4![]() ,0)或(4-4
,0)或(4-4![]() ,0),
,0),
综上所述,Q点的坐标为(0,0)或(-4,0)或(4+4![]() ,0)或(4-4
,0)或(4-4![]() ,0).
,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
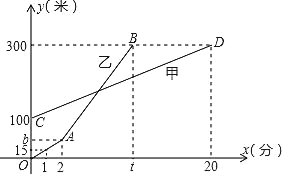
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD为⊙O的内接四边形,直径AC与对角线BD相交于点E,作CH⊥BD于H,CH与过A点的直线相交于点F,∠FAD=∠ABD.
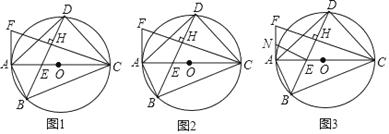
(1)求证:AF为⊙O的切线;
(2)若BD平分∠ABC,求证:DA=DC;
(3)在(2)的条件下,N为AF的中点,连接EN,若∠AED+∠AEN=135°,⊙O的半径为2![]() ,求EN的长.
,求EN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是原点,
是原点,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() .
.
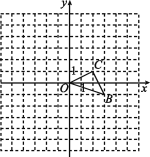
(1)以点![]() 为位似中心,在
为位似中心,在![]() 轴的左侧将
轴的左侧将![]() 扩大为原来的两倍(即新图与原图的相似比为
扩大为原来的两倍(即新图与原图的相似比为![]() ),画出图形,并写出点
),画出图形,并写出点![]() 的对应点的坐标;
的对应点的坐标;
(2)如果![]() 内部一点
内部一点![]() 的坐标为
的坐标为![]() ,写出点
,写出点![]() 的对应点
的对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
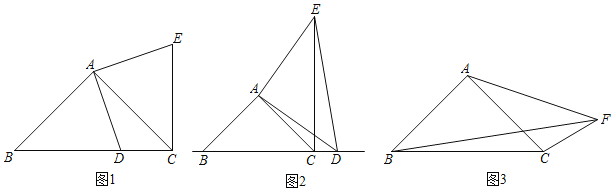
【题目】(1)问题发现:如图1,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B、C重合)将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BD与CE的数量关系是 ,位置关系是 ;
(2)探究证明:如图2,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC的延长线上时,连接EC,写出此时线段AD,BD,CD之间的等量关系,并证明;
(3)拓展延仲:如图3,在四边形ABCF中,∠ABC=∠ACB=∠AFC=45°.若BF=13,CF=5,请直接写出AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
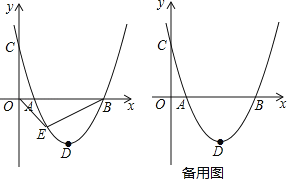
【题目】如图,抛物线经过点A(1,0),B(5,0),C(0,![]() )三点,顶点为D,设点E(x,y)是抛物线上一动点,且在x轴下方.
)三点,顶点为D,设点E(x,y)是抛物线上一动点,且在x轴下方.
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求三角形OEB的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)在y轴上确定一点M,使点M到D、B两点距离之和d=MD+MB最小,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2﹣3(a﹣1)x+2a﹣6(a>0).
(1)求证:抛物线与x轴有两个交点.
(2)设抛物线与x轴的两个交点的横坐标分别为x1,x2(其中x1>x2).若t是关于a的函数、且t=ax2﹣x1,求这个函数的表达式;
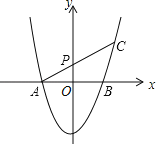
(3)若a=1,将抛物线向上平移一个单位后与x轴交于点A、B.平移后如图所示,过A作直线AC,分别交y的正半轴于点P和抛物线于点C,且OP=1.M是线段AC上一动点,求2MB+MC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
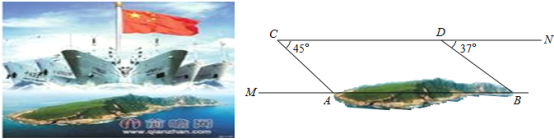
【题目】钓鱼岛是我国固有领土,为测量钓鱼岛东西两端A,B的距离,如图2,我勘测飞机在距海平面垂直高度为1公里的点C处,测得端点A的俯角为45°,然后沿着平行于AB的方向飞行3.2公里到点D,并测得端点B的俯角为37°,求钓鱼岛两端AB的距离.(结果精确到0.1公里,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41)
≈1.41)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com