
分析 (1)由方程有两个实数根,可得出△=8k-12≥0,解之即可得出k的取值范围;
(2)分BC为腰和BC为底两种情况考虑,当BC为腰时,将x=4代入原方程求出k值,将k值代入原方程求出方程的另一个根,利用三角形的三边关系确定该三角形是否存在,再根据三角形的周长公式可求出△ABC的周长;当BC为底时,由根的判别式△=8k-12=0可求出k值,将其代入原方程中求出方程的解,利用三角形的三边关系确定该三角形是否存在,再根据三角形的周长公式可求出△ABC的周长.综上即可得出结论.
解答 解:(1)∵方程有两个实数根,
∴△=[-2(k+1)]2-4(k2+4)=8k-12≥0,
∴k$≥\frac{3}{2}$;
(2)①当BC为腰时,将x=4代入原方程得:16-8(k+1)+k2+4=0,
解得:k=2或k=6.
当k=2时,原方程为x2-6x+8=(x-2)(x-4)=0,
解得:x1=2,x2=4.
∵2、4、4能组成三角形,
∴C△ABC=2+4+4=10;
当k=6时,原方程为x2-14x+40=(x-4)(x-10)=0,
解得:x1=4,x2=10.
∵4、4、10不能组成三角形,
∴k=6舍去;
②当BC为底时,方程x2-2(k+1)x+k2+4=0有两个相等的实数根,
∴△=[-2(k+1)]2-4(k2+4)=8k-12=0,
解得:k=$\frac{3}{2}$.
将k=$\frac{3}{2}$代入原方程得:x2-5x+$\frac{25}{4}$=(x-$\frac{5}{2}$)2=0,
解得:x1=x2=$\frac{5}{2}$.
∵$\frac{5}{2}$、$\frac{5}{2}$、4能组成三角形,
∴C△ABC=$\frac{5}{2}$+$\frac{5}{2}$+4=9.
综上所述:△ABC的周长为9或10.
点评 本题考查了根的判别式,三角形三边关系、等腰三角形的性质以及三角形的周长,解题的关键是:(1)牢记“当△≥0时,方程有两个实数根”;(2)分BC为腰和BC为底两种情况考虑.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
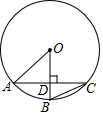 如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )
如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
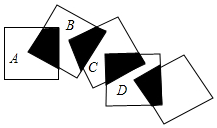 将5个边长都是2cm的正方形如图所示摆放,点A、B、C、D分别是四个正方形对角线的交点,则阴影部分的面积为( )
将5个边长都是2cm的正方形如图所示摆放,点A、B、C、D分别是四个正方形对角线的交点,则阴影部分的面积为( )| A. | 2cm2 | B. | 4cm2 | C. | 6cm2 | D. | 8cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
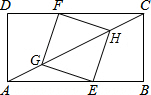 如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$.
如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,EG∥AD,EG⊥HF于I,AB=6cm,AD=10cm,矩形AEIH的面积为2cm2,四边形EBFI的面积为4cm2,则△BIC的面积为( )
如图,矩形ABCD中,EG∥AD,EG⊥HF于I,AB=6cm,AD=10cm,矩形AEIH的面积为2cm2,四边形EBFI的面积为4cm2,则△BIC的面积为( )| A. | 40cm2 | B. | 20cm2 | C. | 10cm2 | D. | 6cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com