
分析 先根据题意设这种彩灯降价x元出售,获利y元,则降价x元后可卖出的总串数为(160+4x),每串获得的利润为(260-x-120),此时根据获得的利润=卖出的总串数×每串彩灯获得的利润,列出二次方程,再根据求二次函数最值的方法求解出获得的最大利润即可.
解答 解:设这种彩灯降价x元出售,获利y元,
则根据题意可得:
y=(260-x-120)(160+4x)=4(-x2+100x+560);
当x=50时,y取得最大值32400元.
即该商场将这种彩灯的售价定为260-50=210元时,每天获利就会最大,最大利润是32400元.
点评 本题考查的是二次函数在实际生活中的应用,解题的关键是从实际问题中抽象出二次函数模型,比较简单.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
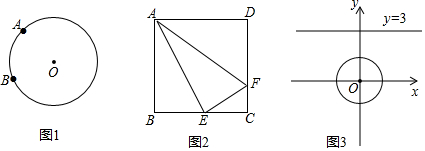
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
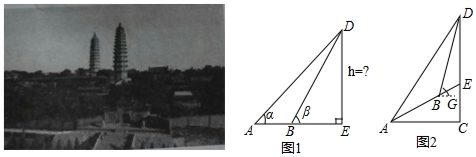
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com