
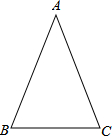
 如图所示,在△ABC中,AB=AC,∠A=36°.
如图所示,在△ABC中,AB=AC,∠A=36°.分析 (1)利用基本作图(作已知角的角平分线)作出BD;
(2)根据等腰三角形的性质和三角形内角和计算出∠ABC=∠C=72°,再利用角平分线的定义得到∠ABD=∠CBD=36°,然后根据等腰三角形的判定得到DA=DB,DB=DC,所以BD=AD.
解答 解:(1)如图所示,BD为所作;
(2)线段DA=BC.理由如下:
∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∴∠ABD=∠A,
∴DA=DB,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD.
点评 本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).


科目:初中数学 来源: 题型:解答题
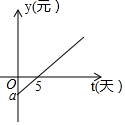 某地蔬菜市场采用如下经营模式:个体蔬菜经营商向市场管理部门租赁摊位,每月缴纳一定的“摊位费”(含市场管理等费用),蔬菜市场管理公司靠收每户的“摊位费”盈利,个体经营商每经营一天,平均可得“营业额”800元,但平均每天要支付蔬菜的“进货费”400元,如图是某个体蔬菜经营商经营一个月(均按30天计算)的收益(除去“摊位费”和“进货费”)y元随经营时间t天变化的函数图象.
某地蔬菜市场采用如下经营模式:个体蔬菜经营商向市场管理部门租赁摊位,每月缴纳一定的“摊位费”(含市场管理等费用),蔬菜市场管理公司靠收每户的“摊位费”盈利,个体经营商每经营一天,平均可得“营业额”800元,但平均每天要支付蔬菜的“进货费”400元,如图是某个体蔬菜经营商经营一个月(均按30天计算)的收益(除去“摊位费”和“进货费”)y元随经营时间t天变化的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
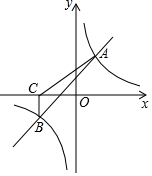 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com