
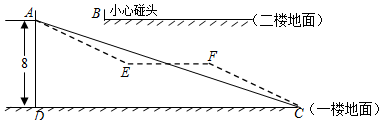
分析 (1)连接AB,作BG⊥AB交AC于点G,在Rt△ABG中,利用已知条件求出AB的长即可;
(2)设直线EF交AD于点P,作CQ⊥EF于点Q,设AP=x,则PE=2x,PD=8-x,在Rt△ACD中利用已知数据可求出CD的长,进而可求出台EF的长度.
解答 解:(1)连接AB,作BG⊥AB交AC于点G,则∠ABG=90°
∵AB∥CD,∴∠BAG=∠ACD=20°,
在Rt△ABG中,$tan∠BAG=\frac{BG}{AB}$,
∵BG=2.26,tan20°≈0.36,
∴$0.36=\frac{2.26}{AB}$,
∴AB≈6.3,
答:A、B之间的距离至少要6.3米.
(2)设直线EF交AD于点P,作CQ⊥EF于点Q,
∵AE和FC的坡度为1:2,
∴$\frac{AP}{PE}=\frac{CQ}{FQ}=\frac{1}{2}$,
设AP=x,则PE=2x,PD=8-x,
∵EF∥DC,
∴CQ=PD=8-x,
∴FQ=2(8-x)=16-2x,
在Rt△ACD中,$tan∠ACD=\frac{AD}{CD}$,
∵AD=8,∠ACD=20°,
∴CD≈22.22
∵PE+EF+FQ=CD,
∴2x+EF+16-2x=22.22,
∴EF=6.22≈6.2
答:平台EF的长度约为6.2米.
点评 此题考查了解直角三角形的应用,用到的知识点是坡度角,关键是根据题意做出辅助线,构造直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com