
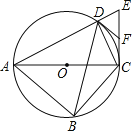
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
【答案】(1)90°;(2)详见解析;(3)2.
【解析】
试题分析:(1)根据圆周角定理即可得∠CDE的度数;(2)连接DO,根据直角三角形的性质和等腰三角形的性质易证∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,即可判定DF是⊙O的切线;(3)根据已知条件易证△CDE∽△ADC,利用相似三角形的性质结合勾股定理表示出AD,DC的长,再利用圆周角定理得出tan∠ABD的值即可.
试题解析:(1)解:∵对角线AC为⊙O的直径,
∴∠ADC=90°,
∴∠EDC=90°;
(2)证明:连接DO,
∵∠EDC=90°,F是EC的中点,
∴DF=FC,
∴∠FDC=∠FCD,
∵OD=OC,
∴∠OCD=∠ODC,
∵∠OCF=90°,
∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,
∴DF是⊙O的切线;
(3)解:如图所示:可得∠ABD=∠ACD,
∵∠E+∠DCE=90°,∠DCA+∠DCE=90°,
∴∠DCA=∠E,
又∵∠ADC=∠CDE=90°,
∴△CDE∽△ADC,
∴![]() =
=![]() ,
,
∴DC2=ADDE
∵AC=2![]() DE,
DE,
∴设DE=x,则AC=2![]() x,
x,
则AC2﹣AD2=ADDE,
期(2![]() x)2﹣AD2=ADx,
x)2﹣AD2=ADx,
整理得:AD2+ADx﹣20x2=0,
解得:AD=4x或﹣4.5x(负数舍去),
则DC=![]() =2x,
=2x,
故tan∠ABD=tan∠ACD=![]() =
=![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】甲、乙两站相距336千米,一列慢车从甲站开出,每小时行驶72千米,一列快车从乙站开出,每小时行驶96千米.
(1)若两车同时相向而行,则几小时后相遇?几小时后相距84千米?
(2)若两车同时反向而行,则几小时后相距672千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是线段AC的中点,N是线段BC的中点.
![]()
(1)如果AC=8cm,BC=6cm,求MN的长.
(2)如果AM=5cm,CN=2cm,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b| .也就是说,|4﹣(﹣3)|表示4与﹣3之差的绝对值,实际上也可理解为4与﹣3两数在数轴上所对的两点之间的距离.
比如|x + 3|可以写成|x﹣(﹣3)|,它的几何意义是数轴上表示数x的点与表示数﹣3的点之间的距离.
再举个例子:等式|x﹣1|=1的几何意义可表示为:在数轴上表示数x的点与表示数1的点的距离等于1,这样的数x可以是0或2.
解决问题
(1) |4﹣(﹣3)|= .
(2)若|x + 3|=7,则x =______;若|x + 3|=|x﹣1|,则x = ______.
(3)| x + 3|+|x﹣1|表示数轴上有理数x所对的点到﹣3和1所对的两点距离之和.请你利用数轴,找出所有符合条件的整数x,使得| x + 3|+|x﹣1|=4.
(4)若![]() 表示一个有理数,则
表示一个有理数,则![]() 有最小值吗?若有,请直接写出最小值.若没有,说出理由。
有最小值吗?若有,请直接写出最小值.若没有,说出理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com