
【题目】对于一个函数,当自变量x取n时,函数值y等于4-n,我们称n为这个函数的“二合点”,如果二次函数y=mx2+x+1有两个相异的二合点x1,x2,且x1<x2<1,则m的取值范围是______.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】甲,乙,丙三个球迷决定通过抓阄来确定谁得到仅有的一张球票,他们准备了三张纸片,纸片上分别写上![]() ,然后将纸片折叠成外观一致的纸团,抓到
,然后将纸片折叠成外观一致的纸团,抓到![]() 纸片的人可以得到球票.
纸片的人可以得到球票.
(1)如果让甲从三张纸团中先抓一张,则甲一次就抓到写![]() 的纸片的概率为 (直接写出答案);
的纸片的概率为 (直接写出答案);
(2)抓阄前,乙产生了疑问:“谁先抓?先抓的人会不会抓中的机会比别人大?”你认为乙的怀疑有没有道理?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/秒的速度移动,同时点Q从B点开始沿BC边向点C以2cm/秒的速度移动,且当其中一点到达终点时,另一个点随之停止移动.
(1)P,Q两点出发几秒后,可使△PBQ的面积为8cm2.
(2)设P,Q两点同时出发移动的时间为t秒,△PBQ的面积为Scm2,请写出S与t的函数关系式,并求出△PBQ面积的最大值.
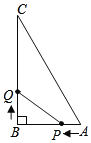
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形OABC的边长为5,且tan∠AOC=![]() ,点E是线段BC的中点,过点A、E的抛物线y=ax2+bx+c与边AB交于点D.
,点E是线段BC的中点,过点A、E的抛物线y=ax2+bx+c与边AB交于点D.
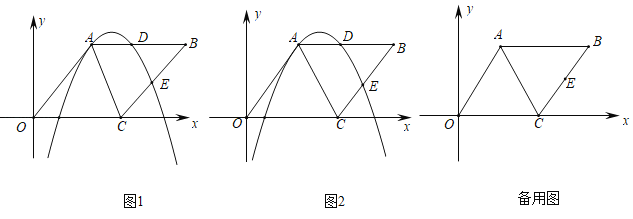
(1)求点A和点E的坐标;
(2)连结DE,将△BDE沿着DE翻折.
①当点B的对应点B'恰好落在线段AC上时,求点D的坐标;
②连接OB、BB',请直接写出此时该抛物线二次项系数a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() x2﹣x+m的图象经过点A(1,﹣2)
x2﹣x+m的图象经过点A(1,﹣2)
(1)求此函数图像与坐标轴的交点坐标;
(2)若P(-2,y1),Q(5,y2)两点在此函数图像上,试比较y1,y2的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径做圆,与BC相切于点C,过点A作AD⊥BO交BO的廷长线于点D,且∠AOD=∠BAD.

(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1.有下列结论:①b2=4ac ②abc>0 ③a>c ④4a+c>2b.其中结论正确的个数是( )
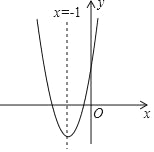
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com