
分析 (1)根据题意可以分别用含x的代数式表示出两种付款的金额;
(2)将x=60分别代入(1)中的代数式,然后比较大小,即可解答本题;
(3)将x=200分别代入(1)中的代数式,然后比较大小,即可解答本题.
解答 解:(1)由题意可得,
方案①付款为:300×50+(x-50)×40=(40x+13000)(元),
方案②付款为:(300×50+40x)×0.9=(13500+36x)(元),
即方案①付款为(40x+13000)元,方案②付款为(13500+36x)元;
(2)当x=60时,
方案①付款为:40x+13000=40×60+13000=15400(元),
方案②付款为:13500+36x=13500+36×60=15660(元),
∵15400<15660,
∴方案①购买较为合算;
(3)当x=200时,
方案①付款为:40x+13000=40×200+13000=21000(元),
方案②付款为:13500+36x=13500+36×200=20700(元),
∵21000>20700,
∴方案②购买较为合算.
点评 本题考查列代数式、代数式求值,解答此类问题的关键是明确题意,列出相应的代数式,会求代数式的值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 水龙头关闭不严就会滴水,现在没拧紧的水龙头下面放一个容器,容器内的盛水量W(L)与滴水时间t(h)的关系如图所示,给合图象解答下列问题:
水龙头关闭不严就会滴水,现在没拧紧的水龙头下面放一个容器,容器内的盛水量W(L)与滴水时间t(h)的关系如图所示,给合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
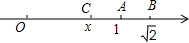 如图所示,数轴上表示1,$\sqrt{2}$的对应点分别为A,B,沿过点A的直线折叠,点B落在数轴上的点C处,设点C所表示的数为x,求$\frac{{x}^{2}+2}{x}$的值.
如图所示,数轴上表示1,$\sqrt{2}$的对应点分别为A,B,沿过点A的直线折叠,点B落在数轴上的点C处,设点C所表示的数为x,求$\frac{{x}^{2}+2}{x}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,4个小动物分别站在正方形场地ABCD的4个顶点处,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
如图,4个小动物分别站在正方形场地ABCD的4个顶点处,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com