练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
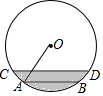
    20．一条排水管的截面如图所示，已知排水管的半径OA=1m，水面宽AB=1.2m，某天下雨后，水管水面上升了0.2m，则此时排水管水面宽为（　　）
    A．1.4mB．1.6mC．1.8mD．2m

    分析 先根据勾股定理求出OE的长，再根据垂径定理求出CF的长，即可得出结论．

    解答 解：如图：作OE⊥AB于E，交CD于F，连接OC．
    ∵AB=1.2m，OE⊥AB，OA=1m，
    ∴OE=0.8m，
    ∵水管水面上升了0.2m，
    ∴OF=0.8-0.2=0.6m，
    ∴CF=$\sqrt{O{C}^{2}-O{F}^{2}}$=0.8m，
    ∴CD=1.6m．
    故选B．

    点评 本题考查的是垂径定理的应用，熟知平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．如图，在Rt△ABC中，∠ACB=90°，AB=6，过点C的直线CF∥AB，D为AB边上一点，DE⊥BC于E交CF于点F．连结BF，CD．
    （1）当点D是AB的中点时，四边形BFCD是什么特殊的四边形？说明你的理由．
    （2）在（1）的条件下，当∠A=45°时，四边形BFCD是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．把抛物线C先向左平移1个单位长度，再向上平移3个单位长度，所得新抛物线的解析式为y=-x2，则抛物线C的解析式为y=-（x-1）2-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，在四边形ABCD中，对角线AC、BD相交于点O，且AO=CO，BO=DO，要使四边形ABCD为矩形，则需添加的条件为∠DAB=90°（填一个即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

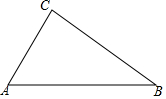    15．如图，在△ABC中，AB＞AC．
    （1）用直尺和圆规作BC的垂直平分线MN（保留作图痕迹，不写作法和证明）；
    （2）若直线MN交AB于点D，连接CD，若AB=6，AC=4，求△ACD的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

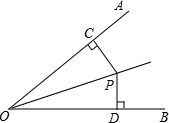    5．如图，OP为∠AOB内的一条射线，PC⊥OA，PD⊥OB，垂足分别是C，D，请添加一个条件OC=OD，使△COP≌△DOP（填一个即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，矩形AOBC的两条边OA，OB的长是方程x2-18x+80=0的两根，其中OA＜OB，沿直线AD将矩形折叠，使点C与y轴上的点E重合．
    （1）求A，B两点的坐标；
    （2）求直线AD的解析式；
    （3）若点P在y轴上，平面内是否存在点Q，使以A，D，P，Q为顶点的四边形为矩形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图甲，点P是半径为6的⊙O外一点，过点P作直线交⊙O于A、B两点，点C是⊙O上一点，连接CP、CA、CB，且PC2=PA•PB．

    （1）求证：PC是⊙O的切线；
    （2）若sin∠ACB=$\frac{{\sqrt{5}}}{3}$，求弦AB的长；
    （3）如图乙，在（2）的条件下，点D是劣弧AB的中点，连接CD交AB于E，若$\frac{AC}{BC}=\frac{1}{3}$，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，其中点B的坐标为（1，0），若抛物线y=x2+k与扇形OAB的边界总有两个公共点，则实数k的取值范围是-1＜k＜$\frac{1}{4}$．

    查看答案和解析>>

    同步练习册答案