
分析 观察$\frac{({2}^{4}+\frac{1}{4})({4}^{4}+\frac{1}{4})({6}^{4}+\frac{1}{4})({8}^{4}+\frac{1}{4})(1{0}^{4}+\frac{1}{4})}{({1}^{4}+\frac{1}{4})({3}^{4}+\frac{1}{4})({5}^{4}+\frac{1}{4})({7}^{4}+\frac{1}{4})({9}^{4}+\frac{1}{4})}$,发现规律:均包含有x4+$\frac{1}{4}$的形式,因而对其进行因式分解得(x2-x+$\frac{1}{2}$)(x2+x+$\frac{1}{2}$).将此规律运用到原式中,通过对分子、分母约分化简,最后求出原式的值.
解答 解:x4+$\frac{1}{4}$=[(x2)2+x2+$\frac{1}{4}$]-x2=(x2+$\frac{1}{2}$)2-x2=(x2+$\frac{1}{2}$+x)(x2+$\frac{1}{2}$-x),
原式=$\frac{\frac{5}{2}×\frac{13}{2}×\frac{25}{2}×\frac{41}{2}×\frac{59}{2}×\frac{85}{2}×\frac{113}{2}×\frac{145}{2}×\frac{181}{2}×\frac{221}{2}}{\frac{1}{2}×\frac{5}{2}×\frac{13}{2}×\frac{25}{2}×\frac{41}{2}×\frac{59}{2}×\frac{85}{2}×\frac{113}{2}×\frac{145}{2}×\frac{181}{2}}$
=$\frac{\frac{221}{2}}{\frac{1}{2}}$=221.
点评 本题考查了有理数无理数的概念与运算,发现规律:均包含有x4+$\frac{1}{4}$的形式,因而对其进行因式分解得(x2-x+$\frac{1}{2}$)(x2+x+$\frac{1}{2}$)是解题关键.


科目:初中数学 来源: 题型:选择题
 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB.则cos∠AOB的值等于( )
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB.则cos∠AOB的值等于( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16和15 | B. | 16和15.5 | C. | 16和16 | D. | 15.5和15.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )
如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )| A. | 2 | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
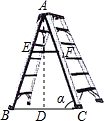 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )| A. | 144cm | B. | 180cm | C. | 240cm | D. | 360cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
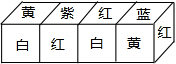 把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:
把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:| 颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
| 花的朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b=2 | B. | b=3 | C. | b=-2 | D. | b=-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com