
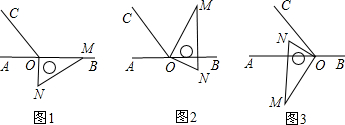
���� ��1���ɽǵ�ƽ���ߵĶ���͵Ƚǵ���������⣻
��2���ɡ�BOC=120��ɵá�AOC=60�㣬���AON=30����NOR=30�㣬��˳ʱ����ת300���120��ʱONƽ�֡�AOC���ݴ���⣻
��3����Ϊ��MON=90�㣬��AOC=60�㣬���ԡ�AOM=90��-��AON����NOC=60��-��AON��Ȼ������ɣ�
��� ��1��ֱ��ONƽ�֡�AOC��
���ɣ�
��ON�ķ����ӳ���ΪOD��
��OMƽ�֡�BOC��
���MOC=��MOB=60�㣬
�֡�OM��ON��
���MON=90�㣬
���BON=30�㣬
���CON=120��+30��=150�㣬
���COD=30�㣬
��ODƽ�֡�AOC��
��ֱ��ONƽ�֡�AOC��
��2���ɣ�1����֪��BON=30�㣬��DON=180��
���ON��ת60���240��ʱֱ��ONƽ�֡�AOC��
������ã�6t=60���240�㣬
��t=10��40��
��3���ߡ�MON=90�㣬��AOC=60�㣬
���AOM=90��-��AON����NOC=60��-��AON��
���AOM-��NOC=��90��-��AON��-��60��-��AON��=30�㣮
���� ���⿼���˽ǵļ��㣬�ؼ���Ӧ���������Ⲣ��ϸ�۲�ͼ�Σ��ҵ�������֮��Ĺ�ϵ���ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 81cm2 | B�� | 18cm2 | C�� | 324cm2 | D�� | 326cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ֱ�������� | B�� | �ȱ������� | C�� | ֱ�������� | D�� | ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���������� | B�� | �ȱ������� | C�� | ֱ�������� | D�� | ����ֱ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com