
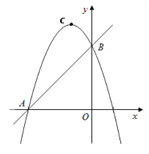
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() (点
(点![]() 与点
与点![]() 不重合),抛物线
不重合),抛物线![]() 经过点
经过点![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
(1)![]() °;
°;
(2)求![]() 的值;
的值;
(3)在抛物线上是否存在点![]() ,能够使
,能够使![]() ?如果存在,请求出点
?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)45;(2)![]() ;(3)
;(3)![]() 的坐标是
的坐标是![]() 或
或![]() .
.
【解析】试题分析(1)直线![]() 是直线y=x平移得到的, y=x是一、三象限的角平分线,所以与x轴的夹角时45°,故能求出
是直线y=x平移得到的, y=x是一、三象限的角平分线,所以与x轴的夹角时45°,故能求出![]() 的度数.
的度数.
(2)首先用n表示出A、B两点的坐标,代入抛物线![]() ,即可求出c和n的值,从而求出抛物线的解析式和顶点C的坐标,根据勾股定理的逆定理证得△ABC是直角三角形,分别求出BCHE AB的长就能求出
,即可求出c和n的值,从而求出抛物线的解析式和顶点C的坐标,根据勾股定理的逆定理证得△ABC是直角三角形,分别求出BCHE AB的长就能求出![]() 的值;
的值;
(3)分两种情况,①当点![]() 在
在![]() 左侧时,过点C作AB的平行线与抛物线的交点即为点P; ②当点
左侧时,过点C作AB的平行线与抛物线的交点即为点P; ②当点![]() 在
在![]() 右侧时,过点
右侧时,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,依据
,依据![]() ∽
∽![]() 求出F点的坐标,易求得直线
求出F点的坐标,易求得直线![]() 的解析式,直线
的解析式,直线![]() 与抛物线的交点即为P点坐标.
与抛物线的交点即为P点坐标.
试题解析:
(1)45 ;
(2)对于直线![]() ,
,
令![]() ,则
,则![]() ,即
,即![]() , 令
, 令![]() ,则
,则![]() ,即
,即![]() ,
,
∵抛物线![]() 经过点
经过点![]()

∴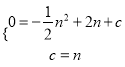 ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
∴![]() ,
, ![]() ,直线为
,直线为![]() ,
,
抛物线为![]() ,
,
∴抛物线的顶点为![]()
设抛物线的对称轴为直线![]() ,连结
,连结![]()
过点![]() 作
作![]() ,则
,则![]() ,
, ![]() ∥
∥![]() 轴
轴
∴![]()
又![]() ∥
∥![]() 轴
轴
∴![]()
∴![]()
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]()
∴在Rt△ABC中, ![]() .
.
(3)①当点![]() 在
在![]() 左侧时,如图,
左侧时,如图,
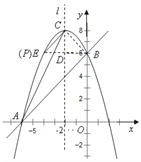
延长![]() 交抛物线于点
交抛物线于点![]() ,当
,当![]() 时,
时, ![]() ∥
∥![]() ,
,
此时,点![]() 与点
与点![]() 重合,点
重合,点![]() 的坐标是
的坐标是![]() ,
,
②当点![]() 在
在![]() 右侧时,如图,
右侧时,如图,

过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,
,
过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,
,
由于![]() ,所以
,所以![]()
∵![]() ∽
∽![]()
∴![]() ,
, ![]() ,
, ![]() ,
, ![]()
∴![]()
易求得直线![]() 的解析式为:
的解析式为: ![]()
由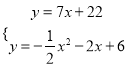 ,消去
,消去![]() ,得
,得![]()
解得![]() 或
或![]() (舍去),因此点
(舍去),因此点![]() 的坐标
的坐标![]() .
.
综上所述, ![]() 的坐标是
的坐标是![]() 或
或![]() .
.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,正确的命题个数为( )
①所有的等腰三角形都相似;
②有一对锐角相等的两个直角三角形相似;
③所有的正方形都相似;
④四个角对应相等的两个梯形相似.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月某日,重庆部分区县的最高温度如下表所示:
地区 | 合川 | 永川 | 江津 | 涪陵 | 丰都 | 梁平 | 云阳 | 黔江 |
温度(℃) | 25 | 26 | 29 | 26 | 24 | 28 | 28 | 29 |
则这组数据的中位数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖在二次函数y=2x2+4x+5的图象上,依横坐标找到三点(﹣1,y1),(2,y2),(﹣3,y3),则你认为y1 , y2 , y3的大小关系应为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某点从数轴上的A点出发,第1次向右移动1个单位长度至B点,第2次从B点向左移动2个单位长度至C点,第3次从C点向右移动3个单位长度至D点,第4次从D点向左移动4个单位长度至E点,…,依此类推,经过_____次移动后该点到原点的距离为2018个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,已知AB=AC,∠A=30°,AB的垂直平分线交AC于D,则∠CBD的度数为( ) 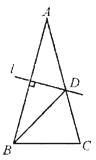
A.50°
B.30°
C.75°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商店将A品牌彩电按成本价提高50%,然后在广告上写“大酬宾,八折优惠”,结果每台A品牌彩电仍获利300元,则每台A品牌彩电的成本价是_____元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com