
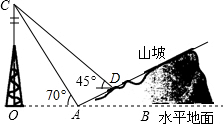
 如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41)
如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41) 分析 作DE⊥OB于点E,DF⊥CO于点F,在Rt△AOC中,根据CO=AO•tan70°,求出CO,设DE=x米,得出AE=2x,在Rt△DCF中,根据∠CDF=45°,得出CF=CO-FO=DF=OA+AE,求出x的值,再根据CF=CO-FO,求出CF,最后根据CD=$\frac{CF}{sin45°}$,求出C与坐台D的距离即可.
解答 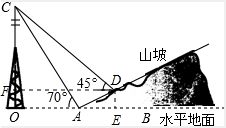 解:作DE⊥OB于点E,DF⊥CO于点F,
解:作DE⊥OB于点E,DF⊥CO于点F,
在Rt△AOC中,AO=200,∠CAO=70°,
∴CO=AO•tan70°=550(米).
设DE=x米,
∵tan∠DAB=$\frac{DE}{AE}$=$\frac{1}{2}$,
∴AE=2x,
在Rt△DCF中,∠CDF=45°,CF=CO-FO=550-x,DF=OA+AE=200+2x,
∵DF=CF,
∴550-x=200+2x,
解得:x=$\frac{350}{3}$≈167(米),
∴CF=CO-FO=550-167=383(米),
∴CD=$\frac{CF}{sin45°}$=$\frac{383}{\frac{\sqrt{2}}{2}}$≈543(米).
答:信号塔塔尖OC高为550米,C与坐台D的距离是543米.
点评 本题考查的知识点是解直角三角形的应用,关键要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
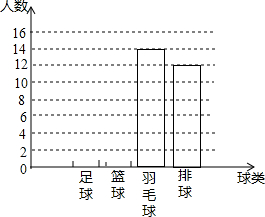 为了了解某校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、羽毛球、排球等四个方面调查了若干名学生,并绘制成不完整的条形图.已知最喜欢篮球的人数占调查人数的32%,最喜欢排球的人数是最喜欢足球人数的1.5倍.
为了了解某校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、羽毛球、排球等四个方面调查了若干名学生,并绘制成不完整的条形图.已知最喜欢篮球的人数占调查人数的32%,最喜欢排球的人数是最喜欢足球人数的1.5倍.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
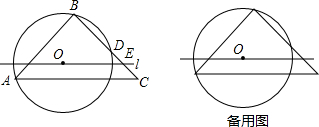
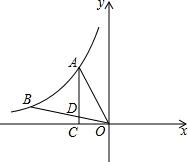 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )| A. | 1 | B. | -$\frac{8}{3}$ | C. | -$\frac{9}{8}$ | D. | -$\frac{9}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
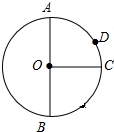 AB是⊙O的直径,且AB=2,OC⊥AB,垂足为点O,弧AD:弧DC=2:1,在OC上有一动点P,则PA+PD的最小值为$\sqrt{3}$.
AB是⊙O的直径,且AB=2,OC⊥AB,垂足为点O,弧AD:弧DC=2:1,在OC上有一动点P,则PA+PD的最小值为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
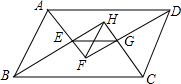 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
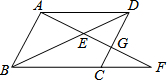 如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$.
如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y<0 | B. | -3<y<-1 | C. | -6<y<-2 | D. | 2<y<6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com