
【题目】甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在同一次测试中,从两校各随机抽取了30名学生的测试成绩进行调査分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.
甲校 | 54 | 68 | 69 | 76 | 76 | 76 | 76 | 77 | 79 | 82 | 83 | 83 | 84 | 84 | 87 |
87 | 87 | 88 | 88 | 89 | 89 | 89 | 89 | 89 | 90 | 92 | 92 | 92 | 93 | 94 | |
乙校 | 57 | 61 | 63 | 71 | 72 | 73 | 76 | 79 | 80 | 83 | 84 | 84 | 84 | 85 | 85 |
87 | 87 | 88 | 89 | 89 | 90 | 90 | 91 | 92 | 92 | 92 | 92 | 92 | 94 | 94 |
(1)请根据乙校的数据补全条形统计图;

(2)两组样本数据的平均数、中位数、众数如下表所示,请补全表格;
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,请为他们各写出一条可以使用的理由;甲校: ;乙校; .
(4)综合来看,可以推断出 校学生的数学学业水平更好一些,理由为 .
【答案】(1)见解析;(2)见解析;(3)平均数、中位数都比乙校高;众数比甲校高,高分的人数多;(4)甲,甲校的平均数、中位数都比乙校高.
【解析】
(1)根据表格中的数据可以得到乙校6069的和7079的各有多少人,从而可以将条形统计图补充完整;
(2)根据表格中的数据将乙校的数据按照从小到大排列,即可得到这组数据的中位数和众数;
(3)可以从平均数、中位数分析甲校,从众数分析乙校,(答案不唯一);
(4)可从平均数、中位数分析判断甲校的成绩较好(答案不唯一).
解:(1)60﹣69的有2人,70﹣79的有12人,补全的条形统计图如图所示:

(2)乙校出现次数最多的是92,众数是92,排序后处在第15,16位的两个数的平均数为(85+87)÷2=86,因此中位数是86,补全的统计表如下:

(3)甲校:平均数、中位数都比乙校高,
乙校:众数比甲校高,高分的人数多,
(4)甲校的成绩较好,甲校的平均数、中位数都比乙校高,
故答案为甲,甲校的平均数、中位数都比乙校高.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】已知y=ax2+bx+c. 当x=1时,y=0;当x=2时,y=4;当x=3时,y=10.
(1)求a、b、c的值;
(2)求x=4时,y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
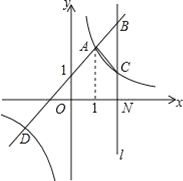
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
查看答案和解析>>
科目:初中数学 来源: 题型:
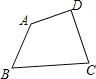
【题目】如图,已知四边形纸片ABCD,现将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线最多有两条,能否做到: (用“能”或“不能”填空).若“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.方法或理由: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AD=9cm,CD=![]() cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)

(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块矩形铁皮,长110cm,宽70cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖的方盒,如果要制作的无盖的方盒的底面积为4500cm2,那么铁皮各角应切去的正方形边长是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:① DC = BC; ②AD+AB=AC.请你证明结论②;
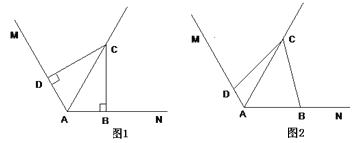
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com