
【题目】如图,抛物线y=ax2+bx(a≠0)的图象过原点O和点A(1, ![]() ),且与x轴交于点B,△AOB的面积为
),且与x轴交于点B,△AOB的面积为![]() 。
。
(1)求抛物线的解析式;
(2)若抛物线的对称轴上存在一点M,使△AOM的周长最小,求M点的坐标;
(3)点F是x轴上一动点,过F作x轴的垂线,交直线AB于点E,交抛物线于点P,且PE=![]() ,直接写出点E的坐标(写出符合条件的两个点即可)。
,直接写出点E的坐标(写出符合条件的两个点即可)。


【答案】(1)![]() ;(2)M(
;(2)M(![]() ,
, ![]() );(3)(下列四个中任意两个正确)(0,
);(3)(下列四个中任意两个正确)(0, ![]() )(
)(![]() ,
, ![]() )(
)(![]() ,
, ![]() )(
)(![]() ,
, ![]() )
)
【解析】试题分析:(1)由△AOB的面积得到OB的长,进而得出点B的坐标.再把A、B的坐标代入抛物线的解析式,解方程组即可得出结论;
(2)先求出抛物线的对称轴,由点B与点O关于对称轴对称,得到直线AB与对称轴的交点就是所要求的点M.由直线AB过A、B两点,得到直线AB的解析式,再求出直线AB和对称轴的交点即可;
(3)设F(x,0),表示出E,P的坐标,进而得到PE的长,解方程即可得出结论.
试题解析:解:(1)∵△AOB的面积为![]() , 点A(1,
, 点A(1, ![]() ),∴
),∴![]() =
=![]() ,∴OB=2,∴B(-2,0).∵抛物线过点A,B,∴
,∴OB=2,∴B(-2,0).∵抛物线过点A,B,∴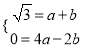 ,解得:
,解得: 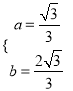 ,∴
,∴![]() ;
;
(2)抛物线的对称轴为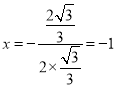 .∵点B与点O关于对称轴
.∵点B与点O关于对称轴![]() 对称,∴由题意得直线AB与对称轴的交点就是点M.设直线AB为:
对称,∴由题意得直线AB与对称轴的交点就是点M.设直线AB为: ![]() .∵直线AB过A、B两点,∴
.∵直线AB过A、B两点,∴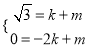 ,解得:
,解得: 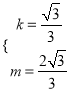 ,∴
,∴![]() .
.
当![]() 时,
时, ![]() ,∴M(
,∴M(![]() ,
, ![]() );
);
(3)设F(x,0),则E(x, ![]() ),P(x,
),P(x, ![]() ),则PE=
),则PE=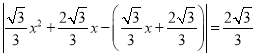 ,整理得:
,整理得: ![]() ,∴
,∴![]() 或
或![]() ,解得:x1=0,x2=-1,x3=
,解得:x1=0,x2=-1,x3=![]() ,x4=
,x4=![]() .∴E的坐标为(0,
.∴E的坐标为(0, ![]() )或(
)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 30 | 42 |
租金/(元/辆) | 300 | 400 |
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
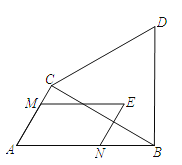
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=6,△BCD为等边三角形,点E为△BCD围成的区域(包括各边)内的一点,过点E作EM∥AB,交直线AC于点M,作EN∥AC,交直线AB于点N,则![]() 的最大值为_____.
的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
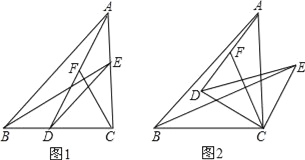
【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则满足下列条件的一定是直角三角形的是( )
A. ∠A:∠B:∠C=3:4:5B. a:b:c=1:![]() :3
:3
C. a=7,b=24,c=25D. a=32,b=42,c=52
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a >0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为![]() ,则a的值是( )
,则a的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
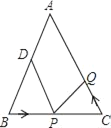
【题目】如图△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,点D为AB的中点.点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为_____ 厘米/秒.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com