
分析 (1)将第一个方程分解因式得:(x+1)(y+3)=0,可得x=-1或y=-3,再分别代入第二个方程中,解出即可;
(2)将第一个方程分解因式得:(x+y)(x-y+1)=0,得到两个一次方程,分别和第二个方程组成新的方程组,解出即可.
解答 解:(1)$\left\{\begin{array}{l}{xy+3x+y+3=0①}\\{3{x}^{2}+4{y}^{2}=12②}\end{array}\right.$,
由①得:x(y+3)+(y+3)=0,
(x+1)(y+3)=0,
x=-1或y=-3.
当x=-1时,3+4y2=12,
4y2=9,y=±$\frac{3}{2}$;
当y=-3时,3x2+36=12,
3x2=-24,
此方程无实数解,
故原方程组的解为$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=\frac{3}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-\frac{3}{2}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{{x}^{2}-{y}^{2}+x+y=0}\\{{x}^{2}-{y}^{2}=2}\end{array}\right.$.
由①得:(x+y)(x-y)+(x+y)=0,
(x+y)(x-y+1)=0,
x+y=0或x-y+1=0,
∴可以化为以下两个方程组:$\left\{\begin{array}{l}{x+y=0①}\\{{x}^{2}-{y}^{2}=2②}\end{array}\right.$,$\left\{\begin{array}{l}{x-y+1=0③}\\{{x}^{2}-{y}^{2}=2④}\end{array}\right.$,
由①和②组成的方程组无解,
解由③和④组成的方程组的解为:$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$,
故原方程组的解为$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$.
点评 本题考查了高次方程组的解法,有难度,此类题都是从一个方程入手,利用将方程变形后分解因式,达到降次的目的,从而解决问题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°,点D在线段AB上,连接CD,∠ADC=60°,AD=2,过C作CE⊥CD,且CE=CD,连接DE,交BC于F.
如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°,点D在线段AB上,连接CD,∠ADC=60°,AD=2,过C作CE⊥CD,且CE=CD,连接DE,交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
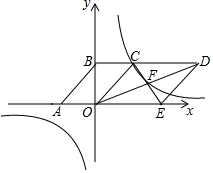 如图,已知反比例函数y=$\frac{1-m}{x}$(m为常数)的图象在平面直角坐标系的第一、三象限,且经过?ABCO的顶点C,点A,B的坐标分别为(-2,0),(0,3),若点P是该反比例函数图象上的一点,且OC=OP,则满足条件的位于第三象限内P点坐标为(-3,-2)或(-2,-3);若该反比例函数图象又经过?COED对角线的交点F,则?COED的面积为18.
如图,已知反比例函数y=$\frac{1-m}{x}$(m为常数)的图象在平面直角坐标系的第一、三象限,且经过?ABCO的顶点C,点A,B的坐标分别为(-2,0),(0,3),若点P是该反比例函数图象上的一点,且OC=OP,则满足条件的位于第三象限内P点坐标为(-3,-2)或(-2,-3);若该反比例函数图象又经过?COED对角线的交点F,则?COED的面积为18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
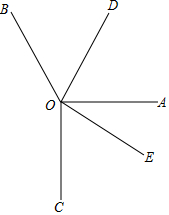 如图,∠AOB=120°,射线OD是∠AOB的角平分线,点C是∠AOB外部一点,且∠AOC=90°,点E是∠AOC内部一点,满足∠AOC=3∠AOE.
如图,∠AOB=120°,射线OD是∠AOB的角平分线,点C是∠AOB外部一点,且∠AOC=90°,点E是∠AOC内部一点,满足∠AOC=3∠AOE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AD=BC | B. | AC=BD | C. | BC∥AD | D. | ∠A=∠B |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com