
分析 (1)原式利用零指数幂、负整数指数幂法则,特殊角的三角函数值,以及绝对值的代数意义化简即可得到结果.
(2)分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出符合条件的x的整数解即可.
解答 解:(1)原式=1-6×$\frac{\sqrt{3}}{3}$+4+$\sqrt{3}$-1
=4-$\sqrt{3}$;
(2)$\left\{\begin{array}{l}{4(x-1)≤3(x+2)①}\\{\frac{x-1}{2}<x-4②}\end{array}\right.$
解不等式①,得x≤10.
解不等式②,得x>7.
∴原不等式组的解集为7<x≤10.
∴原不等式组的所有整数解为8,9,10.
点评 本题考查的是解一元一次不等式组及一元一次不等式组的整数解,能利用数形结合求不等式组的解集是解答此题的关键.也考查了实数的运算,零指数幂、负整数指数幂.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
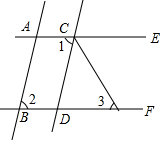 如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题.
如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=2,P是△ABC所在平面内一点,且满足PA⊥PB,则PC的取值范围为$\sqrt{5}$-1≤PC≤$\sqrt{5}$+1.
如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=2,P是△ABC所在平面内一点,且满足PA⊥PB,则PC的取值范围为$\sqrt{5}$-1≤PC≤$\sqrt{5}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com