
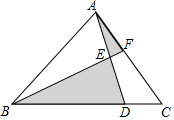
 三角形ABC的面积为10cm2,AE=$\frac{1}{2}$AD,BD=3DC,求阴影部分的面积.
三角形ABC的面积为10cm2,AE=$\frac{1}{2}$AD,BD=3DC,求阴影部分的面积. 分析 连接DF,根据已知条件得到S△AEF=S△DEF,S△ABE=S△BDE,由于BD=3CD,得到S△BDF=3S△CDF,求出S△CDF=$\frac{10}{7}$,于是得到结论.
解答 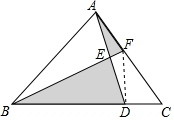 解:连接DF,
解:连接DF,
∵AE=$\frac{1}{2}$AD,
∴S△AEF=S△DEF,S△ABE=S△BDE,
∵BD=3CD,
∴S△BDF=3S△CDF,
∴S△ABF=S△BDF=3S△CDF,
∴S△ABC=7S△CDF,
∴S△CDF=$\frac{10}{7}$,
∴阴影部分的面积=S△BDF=$\frac{30}{7}$.
点评 本题考查了三角形的面积,熟练掌握三角形的面积的求法是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
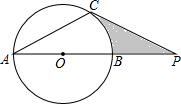 已知如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
已知如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
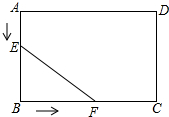 如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.
如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
| 单价(元) | 50 | 40 | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com