
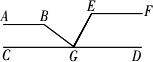
如图,点G在直线CD上,AB∥EF∥CD,且∠ABG∶∠GEF∶∠BGE=4∶3∶2.求∠ABG、∠GEF、∠BGE的度数.
|
分析:观察图形可知,∠CGB+∠BGE+∠EGD=180°.由AB∥CD,EF∥CD,可得∠ABG+∠CGB=180°,∠FEG+∠EGD=180°.根据∠ABG∶∠GEF ∶∠BGE=4∶3∶2,可设∠ABG=4x°,∠GEF=3x°,∠BGE=2x°,并用含x的式子表示出∠BGC和∠EGD的大小,然后列方程求解. 解:设∠ABG=4x°,∠GEF=3x°,∠BGE=2x°. 因为AB∥CD∥EF, 所以∠ABG+∠CGB=180°,∠FEG+∠EGD=180°. 所以∠CGB=180°-4x°,∠EGD=180°-3x°. 又因为∠CGB+∠BGE+∠EGD=180°, 所以(180-4x)+2x+(180-3x)=180.解得x=36. 所以∠ABG=144°,∠FEG=108°,∠BGE=72°. 点评:在涉及到角度的计算问题时,如果已知某些角的度数比,则可借助比值设未知数列方程,通过解方程来解决问题. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:学习周报 数学 华师大七年级版 2009-2010学年 第17期 总第173期 华师大版 题型:044
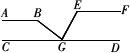
如图,点G在直线CD上,AB∥EF∥CD,且∠ABG∶∠GEF∶∠BGE=4∶3∶2.求∠ABG、∠GEF、∠BGE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com