
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,则下列结论:①
,则下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() 与
与![]() 的面积相等;⑤
的面积相等;⑤![]() ,其中正确的个数是( )
,其中正确的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
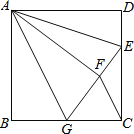
结合条件可证明Rt△ABG≌Rt△AFG,在Rt△EGC中由勾股定理可求得BG=CG=3,BG+CG=6,满足条件,利用外角的性质可求得∠AGB=∠GCF,可得AG∥CF,可求得S△EGC=S△AFE=6,利用多边形的内角和可求得2∠AGB+2∠AED=270°,可得∠AGB+∠AED=135°,所以五个结论都正确.
由正方形![]() 的边长为
的边长为![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,
,
则有DE=2,CE=4,AB=BC=AD=6,
∵将△ADE沿AE对折至△AFE,
∴∠AFE=∠ADE=∠ABG=90°,AF=AD=AB,EF=DE=2,
在Rt△ABG和Rt△AFG中
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),∴①正确;
∴BG=CF,∠BGA=∠FGA,
设BG=GF=x,若BG=CG=x,在Rt△EGC中,EG=x+2,CG=x,CE=4,
由勾股定理可得(x+2)2=x2+42,
解得x=3,此时BG=CG=3,BG+CG=6,满足条件,∴②正确;
∵GC=GF,
∴∠GFC=∠GCF,
且∠BGF=∠GFC+∠GCF=2∠GCF,
∴2∠AGB=2∠GCF,
∴∠AGB=∠GCF,
∴AG∥CF,∴③正确;
∵S△EGC=![]() GCCE=
GCCE=![]() ×3×4=6,S△AFE=
×3×4=6,S△AFE=![]() AFEF=
AFEF=![]() ×6×2=6,
×6×2=6,
∴S△EGC=S△AFE,∴④正确;
在五边形ABGED中,
∠BGE+∠GED=540°-90°-90°-90°=270°,
即2∠AGB+2∠AED=270°,
∴∠AGB+∠AED=135°,∴⑤正确,
∴正确的有五个,
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=22°,则∠B的度数是( ) 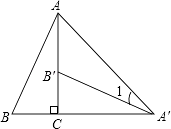
A.67°
B.62°
C.82°
D.72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
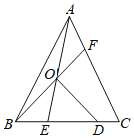
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,点
的等边三角形,点![]() 在
在![]() 上且
上且![]() ,点
,点![]() 从点
从点![]() 出发,向点
出发,向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以相同的速度向点
出发,以相同的速度向点![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 时,运动停止,
时,运动停止,![]() 和
和![]() 相交于点
相交于点![]() ,连接
,连接![]() ,在此过程中线段
,在此过程中线段![]() 长度的最小值是____.
长度的最小值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,
,![]() 在线段
在线段![]() 上,连接
上,连接![]() ,
,![]() 的延长线交
的延长线交![]() 于
于![]() .
.
(1)猜想线段![]() 、
、![]() 的关系;(不必证明)
的关系;(不必证明)
(2)当点![]() 为
为![]() 内部一点时,使点
内部一点时,使点![]() 和点
和点![]() 分别在
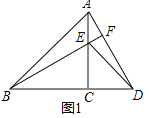
分别在![]() 的两侧,其它条件不变.请你在图2中补全图形,则(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.
的两侧,其它条件不变.请你在图2中补全图形,则(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.
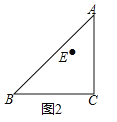
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(﹣1,0)、C(0,﹣3)两点,与x轴交于另一点B.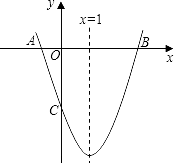
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系: 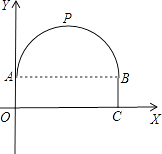
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com