
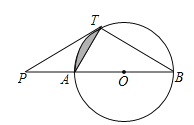
【题目】如图,直线![]() 与
与![]() 相切于点T,直线
相切于点T,直线![]() 与
与![]() 相交于
相交于![]() 两点,连接
两点,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,请直接写出图中阴影部分的面积(结果保留无理数)
,请直接写出图中阴影部分的面积(结果保留无理数)
【答案】(1)见解析;(2)![]()
【解析】
(1)利用切线的性质得∠OTP=90°,即∠2+∠PTA=90°,再利用圆周角定理得到∠ATB=90°,则∠2+∠1=90°,然后利用等量代换得到∠PTA=∠B;
(2)利用TP=TB得到∠P=∠B,而∠POT=2∠B,所以∠POT=2∠P,则利用∠OTP=90°可计算出∠P=30°,∠POT=60°,利用含30度的直角三角形三边的关系得到OT=6,△AOT为等边三角形,然后根据扇形的面积公式和图中阴影部分的面积=S扇形AOT-S△AOT进行计算.
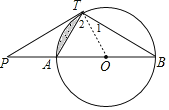
(1)证明:∵直线PT与⊙O相切于点T,
∴OT⊥PT,
∴∠OTP=90°,
即∠2+∠PTA=90°,
∵AB为直径,
∴∠ATB=90°,
∴∠2+∠1=90°,
∴∠PTA=∠1,
∵OB=OT,
∴∠1=∠B,
∴∠PTA=∠B;
(2)解:∵PT=BT,
∴∠P=∠B,
∵∠POT=∠B+∠1=2∠B,
∴∠POT=2∠P,
而∠OTP=90°,
∴∠P=30°,∠POT=60°,
∴OT=![]() PT=6,△AOT为等边三角形,
PT=6,△AOT为等边三角形,
∴图中阴影部分的面积=S扇形AOT-S△AOT=![]() -
-![]() =6π-9
=6π-9![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
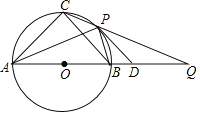
【题目】如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为![]() 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论:①若∠PAB=30°,则
上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论:①若∠PAB=30°,则![]() 的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6
的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6![]() ;④无论点P在
;④无论点P在![]() 上的位置如何变化,CPCQ为定值.其中正确的是________________.(写出所有正确结论的序号)
上的位置如何变化,CPCQ为定值.其中正确的是________________.(写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
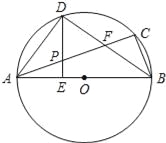
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列4个结论:①abc<0;②2a+b=0;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论的个数是( )
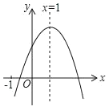
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.
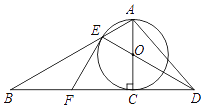
(1)求证:PE是⊙O的切线;
(2)若⊙O的半径为3,∠B=30°,求P点到直线AD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
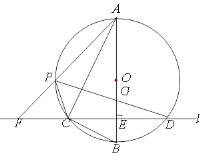
【题目】如图,在⊙O的内接三角形ABC中,![]() ,
,![]() ,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是
,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是![]() 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
(1)求证:![]() ;
;
(2)若![]() ,
, ![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com