练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

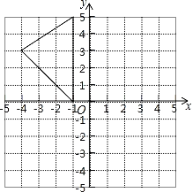
    （1）在图中的点上标出相应字母A、B、C，并求出△ABC的面积；

    （2）在图中作出△ABC关于y轴的对称图形△A1B1C1；

    （3）写出点A1，B1，C1的坐标．

    【答案】（1）如图所示，7.5；（2）如图所示；（3）（1，5），（1，0），（4，3）

    【解析】

    （1）直接利用平面直角坐标系得出各点坐标，求面积时把AB作为底，点C到AB的距离作为高即可；

    分别作出点A、B、C关于y轴的对称的点，然后顺次连接；

    利用关于y轴对称点的性质得出对应点坐标即可；

    解：（1）如图所示，

    三角形ABC的面积为： 53=7.5.

    如图所示，

    （3）∵A（﹣1，5），B（﹣1，0），C（﹣4，3），且点A1，B1，C1与A,B,C关于y轴对称，

    ∴点A1，B1，C1的坐标分别为（1，5），（1，0），（4，3）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】端午节吃粽子是中华民族的传统习惯．农历五月初五早晨，小王的妈妈用不透明袋子装着一些粽子（粽子除食材不同外，其他一切相同），其中糯米粽两个，还有一些薯粉粽，现小王从中任意拿出一个是糯米粽的概率为．

    （1）求袋子中薯粉粽的个数；

    （2）小王第一次任意拿出一个粽子（不放回），第二次再拿出一个粽子，请你用树形图或列表法，求小王两次拿到的都是薯粉粽的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市启动了第二届“美丽港城美在阅读”全民阅读活动．为了解市民每天的阅读时间情况，随机抽取了部分市民进行调查．根据调查结果绘制如下尚不完整的频数分布表：

    (1) 补全表格；

    (2) 将每天阅读时间不低于 的市民称为“阅读爱好者”．若我市约有 万人，请估计我市能称为“阅读爱好者”的市民约有多少万人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．

    （1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；

    （2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？

    （3）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得不低于6000元的利润，那么超市每天至少销售粽子多少盒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把下列各数分别填入相应的集合例

    -2.5，-0.151515…，0，8， ，，，-0.5252252225…（每两个5之间依次增加1个2）

    正数：｛___________________________________________________…｝；

    负分数：｛___________________________________________________…｝；

    整数：｛___________________________________________________…｝．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

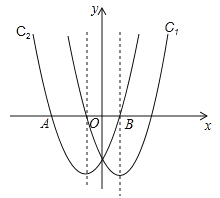
    【题目】在同一直角坐标系中，抛物线y=ax2﹣2x﹣3与抛物线y=x2+mx+n关于y轴对称，C2与x轴交于A、B两点，其中点A在点B的左侧．

    （1）求抛物线C1，C2的函数表达式；

    （2）求A、B两点的坐标；

    （3）在抛物线C1上是否存在一点P，在抛物线C2上是否存在一点Q，使得以AB为边，且以A、B、P、Q四点为顶点的四边形是平行四边形？若存在，求出P、Q两点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

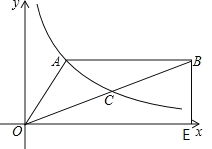
    【题目】如图，双曲线y=（x＞0）经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为（2，3），BE⊥x轴，垂足为E．

    （1）确定k的值；

    （2）若点D（3，m）在双曲线上，求直线AD的解析式；

    （3）计算△OAB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

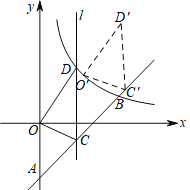
    【题目】如图，一次函数y＝kx－4（k≠0）的图象与y轴交于点A，与反比例函数y＝（x＞0）的图象交于点B（6，b）．

    （1）b＝__________；k＝__________．

    （2）点C是直线AB上的动点（与点A，B不重合），过点C且平行于y轴的直线l交这个反比例函数的图象于点D，当点C的横坐标为3时，得△OCD，现将△OCD沿射线AB方向平移一定的距离（如图），得到△O′C′D′，若点O的对应点O′落在该反比例函数图象上，求点O′，D′的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商品的进价为每件50元．当售价为每件70元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：

    （1）若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；

    （2）当降价多少元时，每星期的利润最大？最大利润是多少？

    查看答案和解析>>

    同步练习册答案