【题目】某采摘农场计划种植A，B两种草莓共6亩，根据表格信息，解答下列问题：
（1）若该农场每年草莓全部被采摘的总收入为460000元，那么A、B两种草莓各种多少亩？
（2）若要求种植A种草莓的亩数不少于种植B种草莓的一半，那么种植A种草莓多少亩时，可使该农场每年草莓全部被采摘的总收入最多？并求出最多总收入．
【答案】(1) A种草莓种植2.5亩，B种草莓种植3.5亩;(2)种植A种草莓2亩时，可使农场每年草莓全部被采摘的总收入最多, 最多为464000元.
【解析】试题分析：
（1）设A种草莓种了
亩，B种草莓种了
亩，根据两种草莓共种了6亩；及农场种植草莓的总收入即可列出方程组，解方程组即可求得所求答案；
（2）设A种草莓种植
亩 ，则由题意可得
，由表中信息可知，A种草莓的亩收益低于B种草莓的亩收益，由此结合
的取值范围即可求得本题答案；
试题解析：
（1）设A种草莓种了
亩，B种草莓种了
亩，由题意可得：
，
解得： 
；
答：A种草莓种植2.5亩，B种草莓种植3.5亩；
（2）设A种草莓种植
亩 ，则由题意可得：
，解得： 
，
由表中信息可得：
A种草莓每亩收益为：60×1200=72000（元）；
B种草莓每亩收益为：40×2000=8000（元）；
∴A种草莓种的越少，B种草莓种的越多，总收益越高，
∴当
，即种A种草莓2亩，B种草莓4亩时，
总收益最高，最高收益为：60×2×1200+40×4×2000=464000（元）.
答：种植A种草莓2亩时，可使农场每年草莓全部被采摘的总收入最多, 最多为464000元.
期末冲刺100分创新金卷完全试卷系列答案科目：初中数学 来源： 题型：
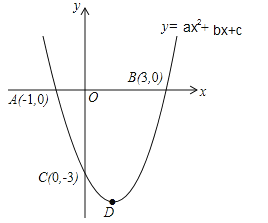
【题目】如图，抛物线
的图象与x轴交于A（﹣1.0），B（3，0）两点，与y轴交于点C（0，﹣3），顶点为D．
（1）求此抛物线的解析式．
（2）求此抛物线顶点D的坐标和对称轴．
（3）探究对称轴上是否存在一点P，使得以点P、D、A为顶点的三角形是等腰三角形？若存在，请求出所有符合条件的P点的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2019年4月17日，国家统计局公布2019年一季度中国经济数据．初步核算，一季度国内生产总值213433亿元，按可比价格计算，同比增长6.4%．数据213433亿用科学记数法表示应为（ ）
A.2.13433×1013B.0.213433×1014
C.213.433×1012D.2.13433×1014
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了传承优秀传统文化，我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛，为了更好地了解本次大赛的成绩分布情况，随机抽取了100名学生的成绩(满分50分)，整理得到如下的统计图表：
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题：
(1)频率统计表中a＝________，b＝_______；
(2)请补全频数分布直方图；
(3)请根据抽样统计结果，估计该次大赛中成绩不低于41分的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某教研机构为了解在校初中生阅读数学教科书的现状，随机抽取某校部分初中学生进行了调查.依据相关数据绘制成以下不完整的统计图表，请根据图表中的信息解答下列问题：
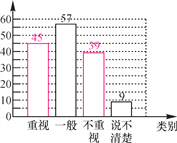
(1)求样本容量及表格中a，b，c的值，并补全统计图；
(2)若该校共有初中生2 300名，请估计该校“不重视阅读数学教科书”的初中生人数；
(3)①根据上面的统计结果，谈谈你对该校初中生阅读数学教科书的现状的看法及建议；
②如果要了解全省初中生阅读数学教科书的情况，你认为应该如何进行抽样？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com