练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】能判定一个四边形是菱形的条件是（ ）

    A. 对角线互相平分且相等 B. 对角线互相垂直且相等

    C. 对角线互相垂直且对角相等 D. 对角线互相垂直，且一条对角线平分一组对角

    【答案】C

    【解析】试题解析：∵对角线互相垂直平分的四边形是菱形，

    ∴A、B、D都不正确；

    ∵对角相等的四边形是平行四边形，而对角线互相垂直的四边形是菱形，

    ∴C正确．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF＝ BC，连结CD和EF.
    （Ⅰ）求证：四边形CDEF是平行四边形；
    （Ⅱ）求四边形BDEF的周长.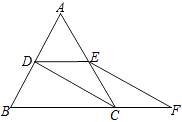

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面上A、B两点间的距离是指（ ）
    A.经过A，B两点的直线
    B.射线AB
    C.A，B两点间的线段
    D.A，B两点间线段长度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若m＞n，下列不等式不一定成立的是（ ）
    A.m﹣2＞n﹣2
    B. ＞
    C.m2＞n2
    D.2m+1＞2n+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△MBN中，BM=6，点A、C、D分别在MB、NB、MN上，四边形ABCD为平行四边形，且∠NDC=∠MDA，则ABCD的周长是（ ）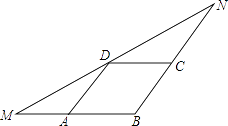
    A.24
    B.18
    C.16
    D.12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【发现证明】

    如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，试判断BE，EF，FD之间的数量关系．

    小聪把△ABE绕点A逆时针旋转90°至△ADG，通过证明△AEF≌△AGF；从而发现并证明了EF=BE+FD．

    【类比引申】

    （1）如图2，点E、F分别在正方形ABCD的边CB、CD的延长线上，∠EAF=45°，连接EF，请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系，并证明；

    【联想拓展】

    （2）如图3，如图，∠BAC=90°，AB=AC，点E、F在边BC上，且∠EAF=45°，若BE=3，EF=5，求CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】心理学家发现：学生对提出概念的接受能力y与提出概念的时间x（min）之间满足二次函数关系y＝﹣0.1x2+2.6x+43．则使学生对概念的接受能力最大．则提出概念的时间应为（　　）

    A. 13minB. 26minC. 52minD. 59.9min

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，中，，，将绕点顺时针旋转得到，当点、、三点共线时，旋转角为，连接，交于点。下面结论：①为等腰三角形；②；③；④中，正确的是（　　）

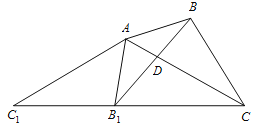
    A. ①③④ B. ①②④ C. ②③④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知⊙O的半径为5厘米，A为线段OP的中点，当OP=6厘米时，点A与⊙O的位置关系是（ ）
    A.点A在⊙O内
    B.点A在⊙O上
    C.点A在⊙O外
    D.不能确定

    查看答案和解析>>

    同步练习册答案