
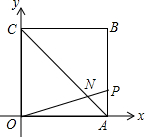
 如图,点A(4,0),C(0,4)在平面直角坐标系中,将△AOC关于AC作轴对称得△ABC.动点P从点A出发,沿折线A→B→C运动至点C停止.连接OP,交AC于点N,则当△AON为等腰三角形时,点P的坐标是
如图,点A(4,0),C(0,4)在平面直角坐标系中,将△AOC关于AC作轴对称得△ABC.动点P从点A出发,沿折线A→B→C运动至点C停止.连接OP,交AC于点N,则当△AON为等腰三角形时,点P的坐标是 ,
,| AO2+OC2 |
| 42+42 |
| 2 |
| 2 |
| CP |
| AO |
| CN |
| AN |
| CP |
| 4 |
4
| ||
| 4 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
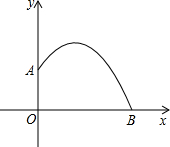 北京时间5月18日-25日,2014年世界羽联汤姆斯杯尤伯杯决赛在印度首都新德里进行,在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-
北京时间5月18日-25日,2014年世界羽联汤姆斯杯尤伯杯决赛在印度首都新德里进行,在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-| 1 |
| 4 |
| 3 |
| 4 |
| A、出球点A离地面点O的距离是1m | ||
| B、该羽毛球横向飞出的最远距离是3m | ||
C、此次羽毛球最高可达到
| ||
D、当羽毛球横向飞出
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com