(本小题满分6分)
小明在研究了苏科版《有趣的坐标系》后,得到启发,针对正六边形OABCDE,自己设计了一个坐标系如图。该坐标系以O为原点,直线OA为x轴,以正六边形OABCDE的边长为一个单位长。坐标系中的任意一点P用一有序实数对(a,b)来表示,我们称这个有序实数对(a,b)为P点的坐标。坐标系中点的坐标的确定方法如下:
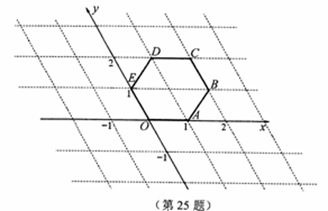
(1)x轴上点M的坐标为(m,0),其中m为M在x轴上表示的实数;
(2)y轴上点N的坐标为(0,n),其中n为N点在y轴上表示的实数;
(3)不在x、y轴上的点Q的坐标为(a,b),其中a为过点Q且与y轴平行的直线与x轴的交点在x轴上表示的实数,b为过点Q且与x轴平行饿直线与y轴的交点在y轴上表示的实数。
则:(1)分别写出点A、B、C的坐标;
(2)标出点M(2,3)的位置;
(3)若点K(x,y)为射线OD上任一点,求x与y所满足的关系式





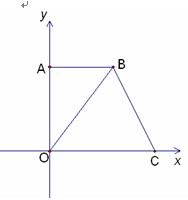
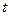 秒(
秒(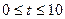 ),
),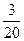 ?若存在,求出
?若存在,求出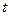
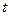 的值或
的值或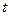 的取值范围
的取值范围