
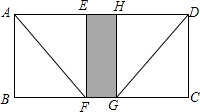
 如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm
如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm分析 (1)由矩形的性质得出AD=BC,AB=DC,由正方形的性质得出AE=BF=AB=EF,DH=CG=DC=HG,即可得出结论;
(2)设EH=xcm,则AD=(x+20)cm;由相似多边形的性质得出对应边成比例$\frac{EH}{AB}=\frac{EF}{AD}$,求出x,即可得出AD的长.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD=BC,AB=DC,
∵四边形ABFE和四边形CDHG是正方形,
∴AE=BF=AB=EF,DH=CG=DC=HG,
∴AE=BF=DH=GC=EF=HG,
∴EH=FG;
(2)解:设EH=xcm,则AD=(x+20)cm;
∵四边形EFGH∽四边形ABCD,
∴$\frac{EH}{AB}=\frac{EF}{AD}$,
即$\frac{x}{10}=\frac{10}{x+20}$,
解得:x=-10±10$\sqrt{2}$(负值舍去),
∴x=-10+10$\sqrt{2}$,
∴AD=-10+10$\sqrt{2}$+20=10+10$\sqrt{2}$(cm).
点评 本题考查了矩形的性质、正方形的性质、相似多边形的性质;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
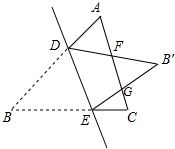 已知△ABC中,AC=BC,点D、E分别在边AB、AC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F、G,若∠ADF=80°,则∠EGC的大小为( )
已知△ABC中,AC=BC,点D、E分别在边AB、AC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F、G,若∠ADF=80°,则∠EGC的大小为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
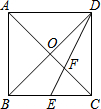 如图,在边长为2的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则EF的长为$\frac{\sqrt{5}}{3}$.
如图,在边长为2的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则EF的长为$\frac{\sqrt{5}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com