
分析 (1)在RT△ABO中,利用勾股定理即可解决.
(2)设点H是△ABC的外接圆的圆心,连接HB、HC、HA,OH交BC于点E,先证明△BHE∽△OAB,得BHAO=BEBO,由dBC=BHBE=AOBO,即可解决问题.
解答 解:(1)如图,∵AB切⊙O于点B,
∴OB⊥AB,
在Rt△ABO中,OB=1,OA=AC+OC=3,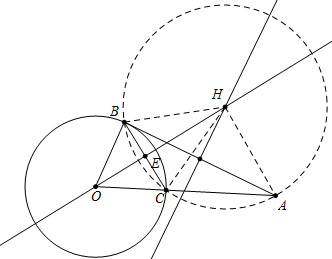
∴AB=√OA2−OB2=2√2;
(2)设点H是△ABC的外接圆的圆心,连接HB、HC、HA,OH交BC于点E,
∵OB=OC,HB=HC,
∴OH垂直平分BC,
∴BE=EC,HE⊥BC,
∴∠BHE=∠CHE,
∴∠CAB=12∠BHC=∠BHE,
∵∠BEH=∠ABO=90°,
∴△BHE∽△OAB,
∴BHAO=BEBO,
∵AC=nOC,
∴BHBE=AOBO=OC+nOCOc=n+1,
∴dBC=BHBE=n+1.
点评 本题考查切线的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
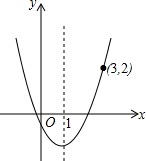 已知函数y=ax2+bx-1的图象经过点(3,2),对称轴为直线x=1.
已知函数y=ax2+bx-1的图象经过点(3,2),对称轴为直线x=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
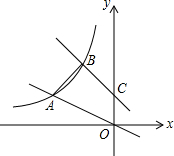 直线y=-x+1交y轴于C点,直线y=-12x,两条直线分别交双曲线y=kx(x<0)于B、A两点,若OABC=√102.
直线y=-x+1交y轴于C点,直线y=-12x,两条直线分别交双曲线y=kx(x<0)于B、A两点,若OABC=√102.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
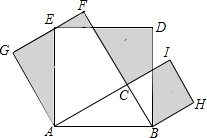 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )| A. | 60 | B. | 90 | C. | 144 | D. | 169 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
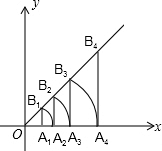 如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )| A. | (√2)n-1 | B. | (√2)n | C. | (√2)n+1 | D. | 2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com