
°ĺŐ‚ńŅ°ŅĹ‚īūŌ¬Ń–ő Ő‚£ļ
£®1£©‘ń∂ŃņŪĹ‚£ļ
»ÁÕľ1£¨‘ŕ![]() ÷–£¨»Ű
÷–£¨»Ű![]() £¨
£¨![]() £¨«ů
£¨«ů![]() ĪŖ…ŌĶń÷–ŌŖ
ĪŖ…ŌĶń÷–ŌŖ![]() Ķń»°÷Ķ∑∂őß.
Ķń»°÷Ķ∑∂őß.
Ĺ‚ĺŲīňő Ő‚Ņ…“‘”√»ÁŌ¬∑Ĺ∑®£ļ—”≥§![]() ĶĹĶ„
ĶĹĶ„![]() Ļ
Ļ![]() £¨‘ŔѨŔ
£¨‘ŔѨŔ![]() £®ĽÚĹę
£®ĽÚĹę![]() »∆◊Ň
»∆◊Ň![]() ńś Ī’Ž–ż◊™
ńś Ī’Ž–ż◊™![]() Ķ√ĶĹ
Ķ√ĶĹ![]() £¨į—
£¨į—![]() °Ę
°Ę![]() £¨
£¨![]() ľĮ÷–‘ŕ
ľĮ÷–‘ŕ![]() ÷–£¨ņŻ”√»żĹ«–ő»żĪŖĶńĻōŌĶľīŅ…Ň–∂Ō.÷–ŌŖ
÷–£¨ņŻ”√»żĹ«–ő»żĪŖĶńĻōŌĶľīŅ…Ň–∂Ō.÷–ŌŖ![]() Ķń»°÷Ķ∑∂őß «______.
Ķń»°÷Ķ∑∂őß «______.
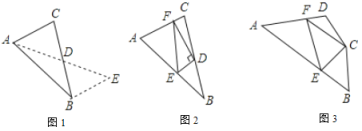
£®2£©ő Ő‚Ĺ‚ĺŲ£ļ
»ÁÕľ2£¨‘ŕ![]() ÷–£¨
÷–£¨![]() «
«![]() ĪŖ…ŌĶń÷–Ķ„£¨
ĪŖ…ŌĶń÷–Ķ„£¨![]() ”ŕĶ„
”ŕĶ„![]() £¨
£¨![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨
£¨![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨«ů÷§£ļ
£¨«ů÷§£ļ![]() .
.
£®3£©ő Ő‚Õō’Ļ£ļ
»ÁÕľ3£¨‘ŕňńĪŖ–ő![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨“‘
£¨“‘![]() ő™∂•Ķ„◊ų“ĽłŲ
ő™∂•Ķ„◊ų“ĽłŲ![]() Ĺ«£¨Ĺ«ĶńŃĹĪŖ∑÷ĪūĹĽ
Ĺ«£¨Ĺ«ĶńŃĹĪŖ∑÷ĪūĹĽ![]() £¨
£¨![]() ”ŕ
”ŕ![]() °Ę
°Ę![]() ŃĹĶ„£¨Ń¨Ĺ”
ŃĹĶ„£¨Ń¨Ĺ”![]() £¨ŐĹňųŌŖ∂ő
£¨ŐĹňųŌŖ∂ő![]() £¨
£¨![]() £¨
£¨![]() ÷ģľšĶń żŃŅĻōŌĶ£¨≤Ęľ”“‘÷§√ų.
÷ģľšĶń żŃŅĻōŌĶ£¨≤Ęľ”“‘÷§√ų.
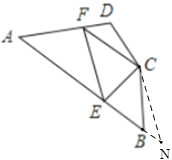
°ĺīūįł°Ņ£®1£©2<AD<8£Ľ£®2£©÷§√ųľŻĹ‚őŲ£Ľ£®3£©EF=BE+DF£¨÷§√ųľŻĹ‚őŲ.
°ĺĹ‚őŲ°Ņ
£®1£©ņŻ”√SASŅ…÷§√ų°ųADC°’°ųEDB£¨Ņ…Ķ√BE=AC=6£¨łýĺ›»żĹ«–ő»żĪŖĻōŌĶľīŅ…Ķ√īūįł£Ľ£®2£©—”≥§FD÷ŃĶ„M£¨ ĻDM=DF£¨Ń¨Ĺ”BM°ĘEM£¨Õ¨£®1£©Ņ…Ķ√CF=BM£¨łýĺ›īĻ÷Ī∆Ĺ∑÷ŌŖ–‘÷ Ņ…Ķ√EF=EM£¨ņŻ”√»żĹ«–ő»żĪŖĻōŌĶľīŅ…Ķ√īūįł£Ľ£®3£©—”≥§AB÷ŃN£¨ ĻBN=DF£¨Ń¨Ĺ”CN£¨Ņ…Ķ√°ŌNBC=°ŌD£¨ņŻ”√SAS÷§√ų°ųNBC°’°ųFDC£¨Ķ√≥ŲCN=CF£¨°ŌNCB=°ŌFCD£¨ņŻ”√Ĺ«ĶńļÕ≤ÓĻōŌĶŅ…Ķ√°ŌECN=70°„=°ŌECF£¨ņŻ”√SAS÷§√ų°ųNCE°’°ųFCE£¨Ķ√≥ŲEN=EF£¨ľīŅ…Ķ√≥ŲĹŠ¬Ř£ģ
£®1£©°ŖCD=BD£¨°ŌADC=°ŌEDB£¨AD=DE£¨
°ŗ°ųADC°’°ųEDB£¨
°ŗBE=AC=6£¨
‘ŕ°ųABE÷–£¨AB-BE<AE<AB+BE£¨ľī10-6<2AD<10+6£¨
°ŗ2<AD<8£¨
Ļ īūįłő™£ļ2<AD<8
£®2£©»ÁÕľ£¨—”≥§FD÷ŃĶ„M£¨ ĻDM=DF£¨Ń¨Ĺ”BM°ĘEM£¨
Õ¨£®1£©Ķ√CF=BM£¨
°ŖFD=MD£¨DE°ÕDF£¨
°ŗEF=EM£¨
‘ŕ°ųBEM÷–£¨BE+BM>EM£¨
°ŗBE+CF>EF.
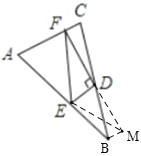
£®3£©EF=BE+DF£¨÷§√ų»ÁŌ¬£ļ
»ÁÕľ£¨—”≥§AB÷ŃN£¨ ĻBN=DF£¨Ń¨Ĺ”CN£¨
°Ŗ°ŌD+°ŌABC=180°„£¨°ŌABC+°ŌNBC=180°„£¨
°ŗ°ŌD=°ŌNBC£¨
‘ŕ°ųNBCļÕ°ųFDC÷–£¨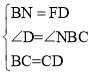 £¨
£¨
°ŗ°ųNBC°’°ųFDC£¨
°ŗCN=CF£¨°ŌNCB=°ŌFCD£¨
°Ŗ°ŌECF=70°„£¨°ŌBCD=140°„£¨
°ŗ°ŌFCD+°ŌECB=70°„£¨
°ŗ°ŌNCB+°ŌECB=70°„£¨ľī°ŌECN=70°„=°ŌECF£¨
‘ŕ°ųFCEļÕ°ųNCE÷–£¨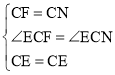 £¨
£¨
°ŗ°ųNCE°’°ųFCE£¨
°ŗEF=EN=BE+BN=BE+DF.


 ∆ŕń©≥ŚīŐ100∑÷īī–¬ĹūĺŪÕÍ»ę ‘ĺŪŌĶŃ–īūįł
∆ŕń©≥ŚīŐ100∑÷īī–¬ĹūĺŪÕÍ»ę ‘ĺŪŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
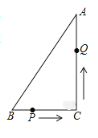
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ°ųABC÷–£¨BC=7cm£¨AC=24cm£¨AB=25cm£¨PĶ„‘ŕBC…Ō£¨ī”BĶ„ĶĹCĶ„‘ň∂Į(≤ĽįŁņ®CĶ„)£¨Ķ„P‘ň∂ĮĶńňŔ∂»ő™2cm/s£ĽQĶ„‘ŕAC…Ōī”CĶ„‘ň∂ĮĶĹAĶ„(≤ĽįŁņ®AĶ„)£¨ňŔ∂»ő™5cm/s£ģ»ŰĶ„P°ĘQ∑÷Īūī”B°ĘCÕ¨ Ī‘ň∂Į£¨«ŽĹ‚īūŌ¬√śĶńő Ő‚£¨≤Ę–ī≥ŲŐĹňų÷ų“™Ļż≥Ő£ļ
£®1£©ĺ≠Ļż∂ŗ…Ŕ Īľšļů£¨P°ĘQŃĹĶ„ĶńĺŗņŽő™5![]() cm£Ņ
cm£Ņ
£®2£©ĺ≠Ļż∂ŗ…Ŕ Īľšļů£¨![]() Ķń√śĽżő™15cm2£Ņ
Ķń√śĽżő™15cm2£Ņ
£®3£©…Ť‘ň∂Į Īľšő™t£¨”√ļ¨tĶńīķ ż ĹĪŪ ĺ°ųPCQĶń√śĽż£¨≤Ę”√Ňš∑Ĺ∑®ňĶ√ųtő™ļő÷Ķ Ī°ųPCQĶń√śĽż◊Óīů£¨◊Óīů√śĽż «∂ŗ…Ŕ£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£ļĶ„E°ĘFő™ŌŖ∂őBDĶńŃĹłŲ»żĶ»∑÷Ķ„£¨ňńĪŖ–őAECF «Ń‚–ő£¨«“Ń‚–őAECFĶń÷‹≥§ő™20£¨BDő™24£¨‘ÚňńĪŖ–őABCDĶń√śĽżő™£® £©
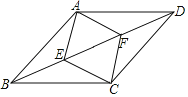
A.24B.36C.72D.144
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™∑÷ Ĺ![]() £¨ ‘Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
£¨ ‘Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
£®1£©∑÷ Ĺ![]() ”–“‚“ŚĶńŐűľĢ « £¨∑÷ Ĺ
”–“‚“ŚĶńŐűľĢ « £¨∑÷ Ĺ![]() ĶńŐűľĢ « £Ľ
ĶńŐűľĢ « £Ľ
‘ń∂Ń≤ńŃŌ£ļ»Ű∑÷ Ĺ![]() Ķń÷Ķīů”ŕ
Ķń÷Ķīů”ŕ![]() £¨‘Ú
£¨‘Ú![]() ĽÚ
ĽÚ![]() £¨
£¨
£®2£©łýĺ›…Ō√ś’‚∂ő‘ń∂Ń≤ńŃŌ£¨»Ű∑÷ Ĺ![]() £¨«ů
£¨«ů![]() Ķń»°÷Ķ∑∂őߣĽ
Ķń»°÷Ķ∑∂őߣĽ
£®3£©łý囓‘…Ōńŕ»›£¨◊‘÷ųŐĹĺŅ£ļ»Ű∑÷ Ĺ![]() £¨«ů
£¨«ů![]() Ķń»°÷Ķ∑∂őß(“™«ů£ļ–ī≥ŲŐĹĺŅĻż≥Ő)£ģ
Ķń»°÷Ķ∑∂őß(“™«ů£ļ–ī≥ŲŐĹĺŅĻż≥Ő)£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
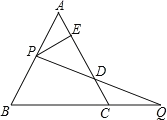
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨ĪŖ≥§ő™![]() ĶńĶ»ĪŖ
ĶńĶ»ĪŖ![]() ÷–£¨“Ľ∂ĮĶ„
÷–£¨“Ľ∂ĮĶ„![]() —ō
—ō![]() ī”
ī”![]() ŌÚ
ŌÚ![]() “∆∂Į£¨∂ĮĶ„
“∆∂Į£¨∂ĮĶ„![]() “‘Õ¨—ýĶńňŔ∂»ī”
“‘Õ¨—ýĶńňŔ∂»ī”![]() ≥Ų∑Ę—ō
≥Ų∑Ę—ō![]() Ķń—”≥§ŌŖ‘ň∂Į£¨Ń¨
Ķń—”≥§ŌŖ‘ň∂Į£¨Ń¨![]() ĹĽ
ĹĽ![]() ĪŖ”ŕ
ĪŖ”ŕ![]() £¨◊ų
£¨◊ų![]() ”ŕ
”ŕ![]() £¨‘Ú
£¨‘Ú![]() Ķń≥§ő™__________£ģ
Ķń≥§ő™__________£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨÷ĪŌŖ![]() ĶńĹ‚őŲĪŪīÔ Ĺő™
ĶńĹ‚őŲĪŪīÔ Ĺő™![]() £¨«“
£¨«“![]() ”Ž
”Ž![]() ÷ŠĹĽ”ŕĶ„
÷ŠĹĽ”ŕĶ„![]() .÷ĪŌŖ
.÷ĪŌŖ![]() ĺ≠ĻżĶ„
ĺ≠ĻżĶ„![]() £¨÷ĪŌŖ
£¨÷ĪŌŖ![]() ĹĽ”ŕĶ„
ĹĽ”ŕĶ„![]() £ģ
£ģ
£®1£©«ůĶ„![]() Ķń◊ÝĪÍ£Ľ
Ķń◊ÝĪÍ£Ľ
£®2£©«ů÷ĪŌŖ![]() ĶńĹ‚őŲĪŪīÔ Ĺ£Ľ
ĶńĹ‚őŲĪŪīÔ Ĺ£Ľ
£®3£©‘ŕ![]() ÷Š…Ō«ů◊ų“ĽĶ„
÷Š…Ō«ů◊ų“ĽĶ„![]() £¨ Ļ
£¨ Ļ![]() ĶńļÕ◊Ó–°£¨÷ĪĹ”–ī≥Ų
ĶńļÕ◊Ó–°£¨÷ĪĹ”–ī≥Ų![]() Ķń◊ÝĪÍ£ģ
Ķń◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
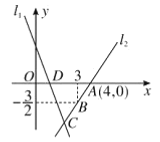
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨“—÷™Ķ„A°ĘBĶń◊ÝĪÍ∑÷Īūő™£®10£¨0£©°Ę£®0£¨4£©£¨C «ABĶń÷–Ķ„£¨ĻżĶ„C◊ųy÷ŠĶńīĻŌŖ£¨īĻ◊„ő™D£¨∂ĮĶ„Pī”Ķ„D≥Ų∑Ę£¨—ōDCŌÚĶ„C“‘√Ņ√Ž1łŲĶ•őĽ‘»ňŔ‘ň∂Į£¨ĻżĶ„P◊ųx÷ŠĶńīĻŌŖ£¨īĻ◊„ő™E£¨Ń¨Ĺ”BP°ĘEC£ģĶĪBPňý‘ŕ÷ĪŌŖ”ŽECňý‘ŕ÷ĪŌŖīĻ÷Ī Ī£¨Ķ„P‘ň∂ĮĶń Īľšő™_____√Ž£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
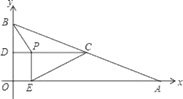
°ĺŐ‚ńŅ°Ņ“—÷™£ļ»ÁÕľ![]() £¨
£¨![]() £¨ń«√ī
£¨ń«√ī![]() ≥…Ńʬū£Ņő™ ≤√ī£ŅŌ¬√ś «–°ņŲÕ¨—ßĹÝ––ĶńÕ∆ņŪ£¨«Žń„Ĺę–°ņŲÕ¨—ßĶńÕ∆ņŪĻż≥Ő≤Ļ≥šÕÍ’Ż£ģ
≥…Ńʬū£Ņő™ ≤√ī£ŅŌ¬√ś «–°ņŲÕ¨—ßĹÝ––ĶńÕ∆ņŪ£¨«Žń„Ĺę–°ņŲÕ¨—ßĶńÕ∆ņŪĻż≥Ő≤Ļ≥šÕÍ’Ż£ģ
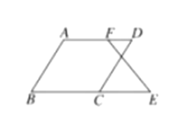
Ĺ‚£ļ≥…ŃĘ£¨ņŪ”…»ÁŌ¬£ļ
![]() £®“—÷™£©
£®“—÷™£©
![]() ĘŔ £®Õ¨Ň‘ńŕĹ«Ľ•≤Ļ£¨ŃĹŐű÷ĪŌŖ∆Ĺ––£©
ĘŔ £®Õ¨Ň‘ńŕĹ«Ľ•≤Ļ£¨ŃĹŐű÷ĪŌŖ∆Ĺ––£©
![]() £®Ęŕ £©
£®Ęŕ £©
”÷![]()
![]() £®“—÷™£©£¨
£®“—÷™£©£¨![]() £®Ķ»ŃŅīķĽĽ£©
£®Ķ»ŃŅīķĽĽ£©
![]() £®ĘŘ £©
£®ĘŘ £©
![]() £®Ę‹ £©£ģ
£®Ę‹ £©£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ∂ĢīőļĮ ży=ax2+bx+c£®a°Ŕ0£©Ķń≤Ņ∑÷ÕľŌů»ÁÕľňý ĺ£¨ÕľŌůĻżĶ„£®©Ā1£¨0£©£¨∂‘≥∆÷Šő™÷ĪŌŖx=2£¨Ō¬Ń–ĹŠ¬Ř£ļ£®1£©4a+b=0£Ľ£®2£©9a+c£ĺ3b£Ľ£®3£©8a+7b+2c£ĺ0£Ľ£®4£©»ŰĶ„A£®©Ā3£¨y1£©°ĘĶ„B£®©Ā![]() £¨y2£©°ĘĶ„C£®
£¨y2£©°ĘĶ„C£®![]() £¨y3£©‘ŕł√ļĮ żÕľŌů…Ō£¨‘Úy1£ľy3£ľy2£Ľ£®5£©»Ű∑Ĺ≥Őa£®x+1£©£®x©Ā5£©=©Ā3ĶńŃĹłýő™x1ļÕx2£¨«“x1£ľx2£¨‘Úx1£ľ©Ā1£ľ5£ľx2£ģ∆š÷–’ż»∑ĶńĹŠ¬Ř”–£®°°°°£©
£¨y3£©‘ŕł√ļĮ żÕľŌů…Ō£¨‘Úy1£ľy3£ľy2£Ľ£®5£©»Ű∑Ĺ≥Őa£®x+1£©£®x©Ā5£©=©Ā3ĶńŃĹłýő™x1ļÕx2£¨«“x1£ľx2£¨‘Úx1£ľ©Ā1£ľ5£ľx2£ģ∆š÷–’ż»∑ĶńĹŠ¬Ř”–£®°°°°£©

A. 2łŲ B. 3łŲ C. 4łŲ D. 5łŲ
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com