练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，△ ABC的角A，B，C所对边分别为a，b，c，点O是△ABC的外心，OD⊥BD于D，OE⊥AC于E，OF⊥AB于F，则OD∶OE∶OF为( )

    A. a∶b∶c B. ：： C. sinA∶sinB∶sinC D. cosA∶cosB∶cosC

    【答案】D

    【解析】如图，连接OA、OB、OC，由圆周角定理和等腰三角形三线合一的性质可得∠BOC=2∠BAC=2∠BOD，所以∠BAC=∠BOD；同理样的方法可得∠BOF=∠BCA，∠AOE=∠ABC；设⊙O的半径为R，根据锐角三角函数的定义可得OD=Rcos∠BOD=Rcos∠BAC，OE=Rcos∠AOE=Rcos∠ABC，OF=Rcos∠BOF=Rcos∠ACB，所以OD：OE：OF=cos∠BAC：cos∠ABC：cos∠ACB，故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知二次函数的图像如图，顶点坐标D为（3， ）。它与轴交于A，B两点（点A在B的左侧），与轴交于C点，且AB的长为12. 动点P从A点出发，沿AB方向以1个单位长度/秒的速度向点B运动，设运动时间为t秒.

    （1）求二次函数的解析式；

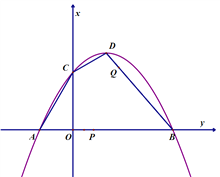
    （2）当△PDB为等腰三角形时，求t的值；

    （3）若动点Q与P同时从A点出发，点Q沿折线ACCDDB运动，在AC，CD，DB上运动的速度分别为3，，2 (个单位长度/秒)﹒当P，Q中的一点到达B点时，两点同时停止运动．连结PQ.

    ①当PQ的中点恰好落在y轴上时，求t的值；

    ②在P，Q的运动过程中，若线段PQ的垂直平分线与线段BD有交点时，请直接写出t的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：关于x的一元二次方程：（m﹣1）x2+（m﹣2）x﹣1=0（m为实数）．

    （1）若方程有两个不相等的实数根，求m的取值范围；

    （2）若是此方程的实数根，抛物线y=（m﹣1）x2+（m﹣2）x﹣1与x轴交于A、B，抛物线的顶点为C，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：x3﹣4xy2=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算中，正确的是（　　）

    A. 2a﹣3a＝aB. a3﹣a2＝aC. 3ab﹣4ab＝﹣abD. 2a+4a＝6a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某企业向银行贷款1000万元，一年后归还银行1065.6多万元，则年利率高于%．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一个长方形的周长为20，其长为a，宽为b，且a，b满足a2-2ab+b2-4a+4b+4=0，求a，b的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市市场交易持续繁荣，市场成交额连续20年居全国各大专业市场榜首.2010年中国小商品城成交额首次突破450亿元关口．请将数据450亿元用科学记数法表示为（ ）（单位：元）
    A.4.50×102
    B.0.45×103
    C.4.50×1010
    D.0.45×1011

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A、B、C、D在⊙O上，O点在∠D的内部，四边形OABC为平行四边形

    (1)求∠D的度数；

    (2)E、F分别是AB、BC上的两点，且AE=CF，延长OE、CB交于点G，求证：∠COF=∠CGO

    (3)在第(2)小题的条件下，连接AC，交OE于点H，若OC=2，CF=1，求OH∶EH∶EG的值．

    查看答案和解析>>

    同步练习册答案