
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;证明: 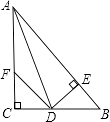
(1)CF=EB.
(2)AB=AF+2EB.
【答案】
(1)证明:∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△CDF和Rt△EDB中,
![]() ,
,
∴Rt△CDF≌Rt△EDB(HL).
∴CF=EB
(2)证明:∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,
![]() ,
,
∴△ADC≌△ADE(HL),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
【解析】(1)根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即CD=DE.再根据Rt△CDF≌Rt△EDB,得CF=EB;(2)利用角平分线性质证明∴△ADC≌△ADE,AC=AE,再将线段AB进行转化.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】星期天小明去逛商场,他发现商场共有四层,第一层有商品a(a+b)种,第二层有(a+b)2种,第三层有b(a+b)种,第四层有(a-b)2种,则这个商场共有多少种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2﹣10ax+c经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,OA= ![]() 且AC=BC.
且AC=BC.
(1)求抛物线的解析式;
(2)如图2,将△AOC沿x轴对折得到△AOC1,再将△AOC1绕平面内某点旋转180°后得△A1O1C2(A,O,C1分别与点A1,O1,C2对应)使点A1,C2在抛物线上,求A1,C2的坐标.
(3)如图3,若Q为直线AB上一点,直接写出|QC﹣QD|的取值范围.
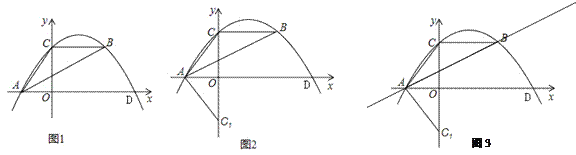
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣2x2先向左平移1个单位,再向下平移3个单位,所得抛物线是( )
A.y=﹣2 (x+1)2+3
B.y=﹣2 (x+1)2﹣3
C.y=﹣2 (x﹣1)2﹣3
D.y=﹣2 (x﹣1)2+3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com