
| 3 | 5 |
| OC |
| AC |
| OG |
| AH |
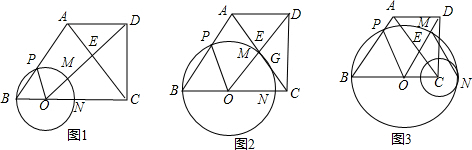
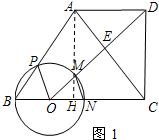 �⣺��1����ͼ1��
�⣺��1����ͼ1��| 3 |
| 5 |
| BH |
| AB |
| 3 |
| 5 |
| OC |
| AC |
| OG |
| AH |
| 6-r |
| 5 |
| r |
| 4 |
| 8 |
| 3 |
| 8 |
| 3 |
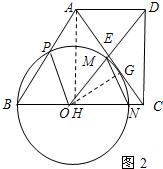
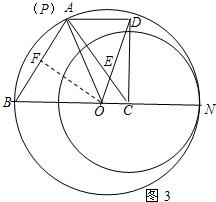 ����O���߶�BC���˶���ʹP��A�غ�ʱ����C�İ뾶CN���
����O���߶�BC���˶���ʹP��A�غ�ʱ����C�İ뾶CN���| 5 |
| 2 |
| 3 |
| 5 |
| BF |
| OB |
| 3 |
| 5 |
| 25 |
| 6 |
| 25 |
| 6 |
| 25 |
| 6 |
| 11 |
| 6 |
| 25 |
| 6 |
| 11 |
| 6 |
| 7 |
| 3 |
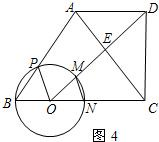 �ڵ�O���߶�BC���˶��Ĺ����У�������MN��AC�������
�ڵ�O���߶�BC���˶��Ĺ����У�������MN��AC�������| OM |
| OE |
| ON |
| OC |
| AD |
| OC |
| DE |
| OE |
| 29 |
| 6 |
| OB |
| AB |
| BP |
| BC |
| r |
| 5 |
| BP |
| 6 |
| 6 |
| 5 |
| 6 |
| 5 |
| 29 |
| 6 |
| 29 |
| 5 |


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
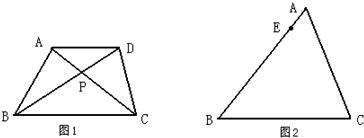
 24����ͼ����֪��AD�ǡ�ABC��BC�ߵ����ߣ���S��ABD=S��ACD��������
24����ͼ����֪��AD�ǡ�ABC��BC�ߵ����ߣ���S��ABD=S��ACD��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| 1 |
| 2 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| AM |
| MB |
| m |
| n |
| bm+an |
| m+n |

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com