
【题目】如图,在等腰Rt△ABC中,AC=BC=2 ![]() ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是
,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是 
【答案】π
【解析】解:取AB的中点O、AE的中点E、BC的中点F,连结OC、OP、OM、OE、OF、EF,如图, 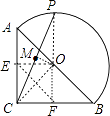
∵在等腰Rt△ABC中,AC=BC=2 ![]() ,
,
∴AB= ![]() BC=4,
BC=4,
∴OC= ![]() AB=2,OP=
AB=2,OP= ![]() AB=2,
AB=2,
∵M为PC的中点,
∴OM⊥PC,
∴∠CMO=90°,
∴点M在以OC为直径的圆上,
点P点在A点时,M点在E点;点P点在B点时,M点在F点,易得四边形CEOF为正方形,EF=OC=2,
∴M点的路径为以EF为直径的半圆,
∴点M运动的路径长= ![]() 2π1=π.
2π1=π.
所以答案是π.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点。已知蚂蚁在爬行过程中保持匀速,且在寻找到食物后停下来吃了2分钟。蚂蚁离出发点的距离s(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)花坛的半径是_______米,蚂蚁是在上述三条线路中的哪条上寻找到了食物_________(填(1)、(2)、或(3));
(2)蚂蚁的速度是_______米/分钟;

(3)蚂蚁从O点出发,直到回到O点,一共用时多少分钟?(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a>0)的顶点为P,其图像与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:
①m=3;
②当∠APB=120°时,a= ![]() ;
;
③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;
④抛物线上存在点N,当△ABN为直角三角形时,有a≥ ![]()
正确的是( )
A.①②
B.③④
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c与y=x的图像如图所示,有以下结论:
①b2﹣4c>0;②3b+c+6=0;③当1<x<3时,x2+(b﹣1)x+c<0;
④ ![]() ,其中正确的有
,其中正确的有
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅客乘车按规定可以随身携带一定重量的行李,如果超过规定,则需要购买行李票,设行李费y(元)与行李重量x(千克)的关系如图,根据图象回答下列问题:
(1)行李重量在________千克以内,不必交费;
(2)当行李重量60千克时,交费____元;
(3)当行李重量________千克时,交费10元;
(4)行李重量每增加1千克,多交_________元;
(5)y= __________ ( y与x之间的关系式)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式的乘法中,能用平方差公式计算的是( )
A. (-m +n)(m - n) B. (![]() a +b)(b -
a +b)(b -![]() a)
a)
C. (x + 5)(x + 5) D. (3a -4b)(3b +4a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°,求AB的高度.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com