
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | 3 |
分析 由已知条件得到OB=|m|,PB=|n|,由PA=1,得到|m|<1,|n|<1,当m,n同号,则|m+n|<2,当m,n异号,则|m+n|<1,于是得到结论.
解答 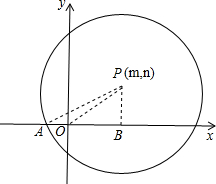 解:如图,∵P(m,n),
解:如图,∵P(m,n),
∴OB=|m|,PB=|n|,
∵PA=1,
∴|m|<1,|n|<1,
∵|2|=2,|-2|=2,|-$\frac{1}{2}$|=$\frac{1}{2}$,|3|=3,
当m,n同号,则|m+n|<2,故m+n不可能A,B,D,
当m,n异号,则|m+n|<1,故m+n不可能A,B,D,
故选C.
点评 本题考查了直线与圆的位置关系,坐标与图形的性质,绝对值的意义,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=8}\\{xy+18=yx}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=8}\\{10(x+y)+18=yx}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=8}\\{10x+y+18=yx}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=8}\\{x+10y+18=10x+y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:
某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
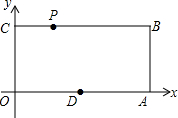 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
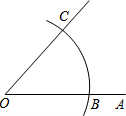 如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com