
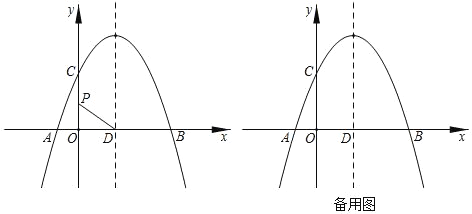
����Ŀ����֪������y��ax2+bx+3������A����1��0����B��3��0��������y�ύ�ڵ�C�������ߵĶԳ�����x�ύ�ڵ�D��
(1)�������ߵĽ���ʽ��
(2)��P��y���������ϵ�һ�����㣬����DP�����߶�DP���ŵ�D˳ʱ����ת90���õ��߶�DE����P�Ķ�Ӧ��Eǡ�������������ϣ������ʱ��P�����ꣻ
(3)��M��m��n�����������ϵ�һ�����㣬����MD����MD2��ʾ���Ա���n�ĺ����������MD2ȡ����Сֵʱ��M�����꣮
���𰸡���1��y����x2+2x+3����2����P������Ϊ��0��1+![]() ������3��MD2��n2��n+4����M������Ϊ��
������3��MD2��n2��n+4����M��������![]() ��
��![]() ������
������![]() ��
��![]() ����
����
��������
��1�����ݵ�A��B�����꣬���ô���ϵ����������������ߵĽ���ʽ����2������E��EF��x���ڵ�F��������ת�����ʼ�ͬ�ǵ������ȣ���֤����ODP�ա�FED��AAS�����������ߵĽ���ʽ�ɵó���D�����꣬�����ɵó�OD�ij��ȣ�����ȫ�������ε����ʿɵó�EF�ij��ȣ������ö��κ���ͼ���ϵ���������������DF��OP�ij�����ϵ�P��y�������ἴ�ɵó���P�����ꣻ��3�����ö��κ���ͼ���ϵ�����������ɵó�m2��2m��3��n�����ݵ�D��M�����꣬���������ľ��빫ʽ�ɵó�MD2��n2��n+4�������䷽���ɵó���MD2ȡ����Сֵʱn��ֵ�������ö��κ���ͼ���ϵ�������������������MD2ȡ����Сֵʱ��M�����꣮
��1����A����1��0����B��3��0������y��ax2+bx+3���ã�![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪy����x2+2x+3��
��2������E��EF��x���ڵ�F����ͼ��ʾ��
�ߡ�OPD+��ODP��90�㣬��ODP+��FDE��90�㣬
���OPD����FDE��
�ڡ�ODP�͡�FED�У�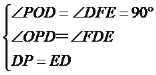 ��
��
���ODP�ա�FED��AAS����
��DF��OP��EF��DO��
�������ߵĽ���ʽΪy����x2+2x+3������x��1��2+4��
���D��������1��0����
��EF��DO��1��
��y��1ʱ����x2+2x+3��1��
��ã�x1��1��![]() ����ȥ����x2��1+
����ȥ����x2��1+![]() ��
��
��DF��OP��1+![]() ��
��
���P��������0��1+![]() ����
����
��3���ߵ�M��m��n�����������ϵ�һ�����㣬
��n����m2+2m+3��
��m2��2m��3��n��
�ߵ�D������Ϊ��1��0����
��MD2����m��1��2+��n��0��2��m2��2m+1+n2��3��n+1+n2��n2��n+4��
��n2��n+4����n��![]() ��2+
��2+![]() ��
��
�൱n��![]() ʱ��MD2ȡ����Сֵ����ʱ��m2+2m+3��
ʱ��MD2ȡ����Сֵ����ʱ��m2+2m+3��![]() ��
��
��ã�m1��![]() ��m2��
��m2��![]() ��
��
��MD2��n2��n+4��
��MD2ȡ����Сֵʱ����M������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ�����װ��4���ʵء���С����ͬ��С����ЩС��ֱ����3��4��5��x����������ÿ��ͬʱ�Ӵ��и��������1��С��������������2��С��������֮�ͣ���¼��С��Żش��н��ȣ������ظ����飬����������ͼ��

����������⣺
��1������������������ȥ�������ϱ����ݣ����֡���Ϊ8����Ƶ�ʽ��ȶ������ĸ��ʸ��������Ƴ��֡���Ϊ8���ĸ����� .
��2�����������������С���ϵ�����֮��Ϊ9�ĸ�����![]() ����ôx��ֵ����ȡ7�������б�������״ͼ��˵������.
����ôx��ֵ����ȡ7�������б�������״ͼ��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�DZ߳�Ϊ1�������Σ���E��AD�����˶����Ҳ����A�͵�D�غϣ�����CE������C��CF��CE��AB���ӳ����ڵ�F��EF��BC�ڵ�G��
��1����֤����CDE�ա�CBF��
��2����DE=![]() ʱ����CG�ij���
ʱ����CG�ij���
��3������AG���ڵ�E�˶������У��ı���CEAG�ܷ�Ϊƽ���ı��Σ����ܣ������ʱDE�ij��������ܣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��a��0����ͼ����ͼ�����н����У���ȷ���۵��У�����������
��b2��4ac��0����abc��0����8a+c��0����9a+3b+c��0��

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=mx2-2mx-3m��m��0����x�ύ��A��B���㣬��y�ύ�ڵ�C����MΪ�����ߵĶ��㣬��OC=OB��
��1���������ߵĽ���ʽ��
��2��������������һ��P����PC���߶�BM��Q�㣬��S��BPQ=S��CMQ����P������꣮
��3������������x��������ƽ��n����λ��ʹƽ�ƺ�������߽�ֱ��BC��E��F���㣬��E��F���ڵ�B�Գƣ���n��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������Ӧ��ί�������ӿ콨������ˮ�̵��̵�������ɳ���ĺ��٣�����ij�ֵ������ӱ�ѡ����������ѡ��һ�ֽ������֣�Ϊ�˸��õ��˽��������⣬������Ա�ڽֵ�Ͻ����Χ�������ȡ�˲��־����С�����ϲ����һ�������ĵ�����ÿ����ѡ����һ�������������������������Ƴ���ͼ������������ͳ��ͼ��
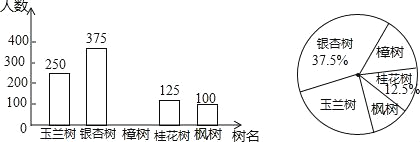
�����������Ϣ����������⣺
��1����β������ľ�������Ϊ���� ����
��2���뽫����ͳ��ͼ����������
��3�����������ͳ��ͼ�С��������������ε�Բ�ĽǶ�����
��4����֪�ýֵ�Ͻ�������о���8���ˣ����������8��������ϲ�����������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB��90�㣬��A��30�㣬����ABC��C�㰴��ʱ�뷽����ת���ǣ�0�㣼����90�㣩�õ���DEC����CD��AB��F������AD����ADF�ǵ�����������ת��������Ϊ��������
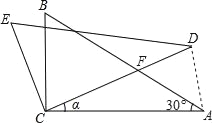
A. 20�� B. 40�� C. 20���40�� D. 60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� XOY=900,OWƽ�֡�XOY��PA��OX��PB ��OY,PC��OW����OA+ OB+OC=1����OC=( )��

A. 2-![]() B.
B. ![]() -1 C.
-1 C. ![]() -2 D. 2
-2 D. 2![]() -3
-3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����PAQ��30�㣬�ڱ�AP��˳�ν�ȡAB��3cm��BC��10cm����BCΪֱ������O������AQ��E��F����������
��1��Բ��O��AQ�ľ�����
��2���߶�EF�ij���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com