练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．一辆列车通过隧道，从车头进车尾出隧道共用1分30秒，已知列车的速度为100千米/时，列车长100米．则隧道长为（　　）
    A．2.5千米B．1.5千米C．2.4千米D．14.9千米

    分析 设隧道长x米，等量关系为：列车速度×相应时间=隧道长+100，把相关数值代入即可求解．

    解答 解：设隧道长x米，
    则x+100=$\frac{100×1000}{60}$×1.5，
    解得：x=2400，
    2400米=2.4千米．
    答：隧道长为2.4千米．
    故选：C．

    点评 此题考查了一元一次方程的应用，解决本题的关键是得到列车1分30秒行驶的路程为隧道长和列车长的和这个等量关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．计算：sin30°cot260°+$\sqrt{2}$sin45°-°$\frac{tan45°}{\sqrt{3}tan60°}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，AB=AC，点D，E分别在AB，AC上，请添加一个条件BD=EC或∠B=∠C，即可推出OD=OE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．已知-2$\frac{2}{5}$×a=1，那么a的值为（　　）
    A．$\frac{5}{12}$B．$-\frac{5}{12}$C．$-\frac{12}{5}$D．$\frac{12}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．按照如图的程序计算，若输入n的值为3时，计算结果为231．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

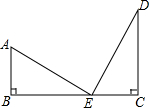    5．如图所示，有两根直杆隔河相对，一杆高30m，另一杆高20m，两杆相距50m．现两杆上各有一只鱼鹰，他们同时看到两杆之间的河面上E处浮起一条小鱼于是以同样的速度同时飞下来夺鱼结果两只鱼鹰同时到达，叼住小鱼．问，两杆底部距鱼的距离各是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知点P是直角坐标平面内一点，点P的坐标为（1，$\sqrt{3}$）．
    （1）点P关于x轴的对称点的坐标为（1，-$\sqrt{3}$）；
    （2）点P关于直线y=x的对称点的坐标为（$\sqrt{3}$，1）；
    （3）线段OP绕原点O旋转90°得到线段OB，则点B的坐标为（$\sqrt{3}$-1）或（-$\sqrt{3}$，1）；
    （4）若△OPQ为等边三角形，则点Q的坐标为（2，0）或（-1，$\sqrt{3}$）；
    （5）若OP为等腰Rt△OPA的腰，且点A在第二象限，则点A的坐标为（-$\sqrt{3}$，1）或（-$\sqrt{3}$+1，1+$\sqrt{3}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．先化简，再求值：已知6x2-3（2x2-4y）+2（x2-y），其中x=-1，y=$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，正方形ABCD的边长为6，E，F分别是AB，BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．
    （1）求证：EF=FM．
    （2）当AE=2时，求EF的长．

    查看答案和解析>>

    同步练习册答案