
分析 (1)应用加减消元法,求出方程组的解是多少即可.
(2)应用代入消元法,求出方程组的解是多少即可.
(3)(4)解一元一次不等式组的方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分,据此求解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-5y=3①}\\{\frac{x}{2}-\frac{y}{3}=1②}\end{array}\right.$
由②,可得:3x-2y=6③,
③-①,可得:3y=3,
解得y=1,
把y=1代入①,解得x=$\frac{8}{3}$,
∴原方程组的解是$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=1}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{3(x+y)-4(x-y)=4①}\\{\frac{x+y}{2}+\frac{x-y}{6}=1②}\end{array}\right.$
由①,可得:x=7y-4③,
把③代入②,解得y=$\frac{11}{15}$,
∴x=7×$\frac{11}{15}$-4=$\frac{17}{15}$,
∴原方程组的解是$\left\{\begin{array}{l}{x=\frac{17}{15}}\\{y=\frac{11}{15}}\end{array}\right.$.
(3)$\left\{\begin{array}{l}{5x-3>2x-9①}\\{1-2x≥-3②}\end{array}\right.$
解不等式①,得x>-2,
解不等式②,得x≤2,
∴这个不等式组的解集是-2<x≤2.
(4)$\left\{\begin{array}{l}{x-3(x-2)>4①}\\{\frac{2x-1}{5}>\frac{x+1}{2}②}\end{array}\right.$
解不等式①,得x<1,
解不等式②,得x<-7,
∴这个不等式组的解集是x<-7.
点评 此题主要考查了解一元一次不等式组的方法,以及解二元一次方程组的方法,要熟练掌握.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
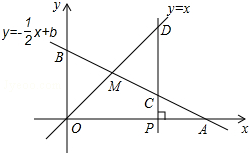 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com