
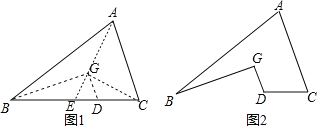
【题目】如图1,G为△ABC纸片的重心,DG∥AC交BC于点D,连结BG,剪去△BGD纸片,剩余部分纸片如图2所示,若原△ABC纸片面积为5,则图2纸片的面积为_____.
【答案】![]() .
.
【解析】
连接AG,延长AG交BD于E,设△DGE的面积为S,利用重心的性质和平行线分线段成比例,用S表示其它三角形的面积,最后得出S△ABC =18S=5,解得S![]() ,可得S△BDG=4S
,可得S△BDG=4S![]() ,即可得图2纸片的面积=5
,即可得图2纸片的面积=5![]() .
.
连接AG,延长AG交BD于E,如图1,设△DGE的面积为S,
∵G为△ABC纸片的重心,
∴BE=CE,AG=2EG,
∵DG∥AC,
∴ED:DC=EG:AG=1:2,
∴S△DGC=2S△DEG=2S,
∴S△BEG=S△CEG=3S,
∴S△ABG=2S△BEG=6S,
∵S△ABE=3S+6S=9S,
∴S△ABC=2S△ABE=18S,
即18S=5,解得S![]() ,
,
∴S△BDG=4S![]() ,
,
∴图2纸片的面积=5![]() .
.
故答案为![]() .
.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:

(1)求本次测试共调查了多少名学生?
(2)求本次测试结果为B等级的学生数,并补全条形统计图;
(3)若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的顶点A,D在直线l上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN,当MN∥B′D′ 时,解答下列问题:
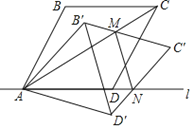
(1)求证:△AB′M≌△AD′N;
(2)求α的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
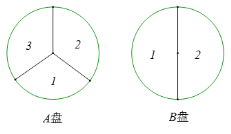
【题目】小辉和小聪两人在玩转盘游戏时,把一个可以自由转动的转盘A成3等份的扇形区域,把转盘B成2等份的扇形区域,并在每一小区内标上数字(如图所示),游戏规则:同时转动两个转盘,当两转盘停止后,若指针所指两个区域的数字之和为2的倍数时,则小辉获胜;若指针所指两个区域的数字之和为3的倍数时,则小聪获胜;如果指针落在分割线上,则需重新转动转盘.在这个游戏中,小辉和小聪两人获胜的概率分别为多少?该游戏规则对双方公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
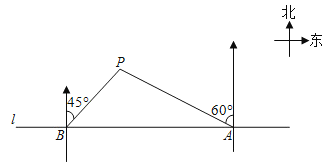
【题目】如图,在一笔直的海岸线L上有A、B两个观测点,A在B的正东方向,AB=2km.有一艘小船在点P处,从A处测得小船在北偏西60°的方向,从B处测得小船在北偏东45°方向.
(1)求P点到海岸线l的距离.
(2)小船从点P处沿射线AP的方向继续行驶,求小船到B处的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=6,AD=8将矩形ABCD沿直线MN翻折后,点B恰好落在边AD上的点E处,如果AE=2AM,那么CN的长为______.
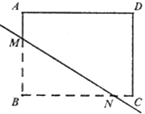
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com