
分析 (1)设售价为x元,根据总利润=单件利润×销售量列方程求解,结合“扩大销售量,减少库存”取舍后可得;
(2)根据(1)中相等关系列出函数解析式,将其配方成顶点式后即可得最值情况.
解答 解:(1)设售价为x元,
根据题意得:(x-30)[600-10(x-40)]=1000,
解得:x=50或x=80,
因扩大销售量,减少库存,
所以x=80舍去,
当x=50时,600-10(x-40)=500,
答:这种台灯的售价应定为50元,这时应进台灯500个;
(2)设每月的销售利润为y元,则
y=(x-30)[600-10(x-40)]=-10x2+1300x-30000=-10(x-65)2+12250,
∴当x=65时,y最大=12250,
此时600-10(x-40)=350个,
答:这种台灯的售价定为65元时,应进台灯350个.
点评 本题主要考查一元二次方程的应用和二次函数的应用,理解题意找到题目蕴含的相等关系是解题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
 某家禽养殖场,用总长为80m的围栏靠墙(墙长为20m)围成如图所示的三块面积相等的矩形区域,设AD长为xm,矩形区域ABCD的面积为ym2.
某家禽养殖场,用总长为80m的围栏靠墙(墙长为20m)围成如图所示的三块面积相等的矩形区域,设AD长为xm,矩形区域ABCD的面积为ym2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
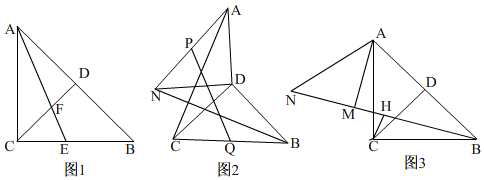
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -3 | -8 | +14 | -10 | +15 | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
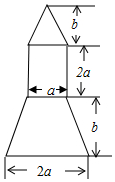 2016年10月17日7时30分,神舟十一号飞船顺利升空,同学们倍受鼓舞,开展了火箭模型制作比赛,如图示是火箭模型的截面图,下面是等腰梯形,中间是长方形,上面是一个等腰三角形.
2016年10月17日7时30分,神舟十一号飞船顺利升空,同学们倍受鼓舞,开展了火箭模型制作比赛,如图示是火箭模型的截面图,下面是等腰梯形,中间是长方形,上面是一个等腰三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com