
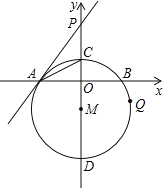
【题目】如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若点C的坐标为(0,2),点A的坐标为(-4,0),
(1)求证:∠PAC=∠CAO;
(2)求直线PA的解析式;
(3)若点Q为⊙M上任意一点,连接OQ、PQ,问![]() 的比值是否发生变化?若不变求出此值;若变化,说明变化规律.
的比值是否发生变化?若不变求出此值;若变化,说明变化规律.
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】
(1)连接MA,如图1,由PA是⊙M的切线得∠PAC+∠MAC=90°;由MA=MC得∠MCA=∠MAC,又∠OAC+∠MCA=90°,易证∠PAC=∠OAC;
(2)如图1,由于点A的坐标已知,要求直线PA的解析式,只需求出点P的坐标,只需求出OP的长,易证△AOM∽△PAM,根据相似三角形的性质可求出MP,从而可求出OP,问题得以解决;
(3)连接MQ,如图2,由于MA=MQ,结合(2)中已证的结论,由此可证到△MOQ∽△MQP,然后运用相似三角形的性质即可解决问题.
(1)连接MA,如图1,

∵PA是⊙M的切线,
∴AM⊥AP,
∴∠PAC+∠MAC=90°,
∵MA=MC,
∴∠MCA=∠MAC,
∵∠OAC+∠MCA=90°,
∴∠PAC=∠OAC;
(2)如图1,
∵∠AMO=∠PMA,∠AOM=∠PAM=90°,
∴△AOM∽△PAM,
∴![]() ,
,
∴MA2=MOMP.
设AM=R,
∵A(-4,0),C(0,2),
∴OA=4,OC=2
在Rt△AOM中,
∵OA=4,OM=R-2,
由AM2=OM2+AO2得,R2=(R-2)2+42
解得,R=5,即AM=5,
∴OM=5-2=3.
∴25=3MP,
∴MP=![]() ,
,
∴OP=MP-OM=![]() -3=
-3=![]() ,
,
∴点P的坐标为(0,![]() ),
),
设直线PA的解析式为y=kx+b,
则有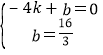 ,
,
解得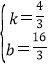 ,
,
∴直线PA的解析式为y=![]() x+
x+![]() ;
;
(3)连接MQ,如图2,
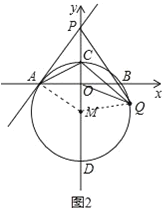
∵![]() ((2)中已证),MA=MQ,
((2)中已证),MA=MQ,
∴![]()
∵∠QMO=∠PMQ,
∴△MOQ∽△MQP,
∴![]() ,
,
∴![]() 不变,等于
不变,等于![]() .
.


科目:初中数学 来源: 题型:
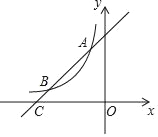
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
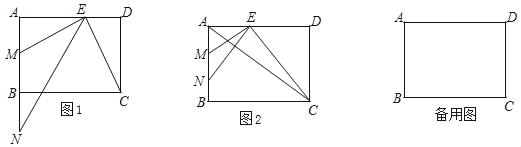
(1)如图1,求证:∠ANE=∠DCE;
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地在进入防汛期间,准备对4800米长的河堤进行加固,在加固工程中,该地驻军出色地完成了任务,它们在加固600米后,采用了新的加固模式,每天加固的长度是原来的2倍,结果只用9天就完成了加固任务.
(1)求该地驻军原来每天加固大坝的米数;
(2)由于汛情严重,该驻军部队又接到了加固一段长4200米大坝的任务,他们以上述新的加固模式进行了2天后,接到命令,必须在4天内完成剩余任务,求该驻军每天至少还要再多加固多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如下(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中D小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
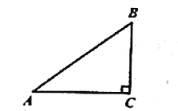
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,先将
,先将![]() 绕着顶点
绕着顶点![]() 顺时针旋转
顺时针旋转![]() ,然后再将旋转后的三角形进行放大或缩小得到
,然后再将旋转后的三角形进行放大或缩小得到![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ),联结
),联结![]() ,如果
,如果![]() 和
和![]() 相似,那么
相似,那么![]() 的长是__________.
的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
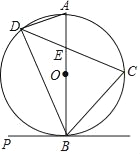
【题目】如图,C、D是以AB为直径的⊙O上的点,![]() ,弦CD交AB于点E.
,弦CD交AB于点E.
(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2﹣CE2=CEDE;
(3)已知OA=4,E是半径OA的中点,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为在中小学生中普及交通法规常识,倡导安全出行,某市教育局在全市范围内组织七年级学生进行了一次“交规记心间”知识竞赛.为了解市七年级学生的竞赛成绩,随机抽取了若干名学生的竞赛成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和图所示的频数分布直方图(频数分布直方图中有一处错误).
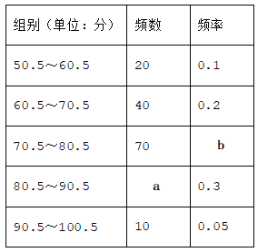
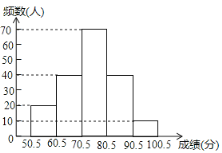
请根据图表信息回答下列问题:
(1)在频数分布表中,![]() ,
,![]() .
.
(2)指出频数分布直方图中的错误,并在上改正;
(3)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问:甲同学的成绩应在什么范围?
(4)全市共有5000名七年级学生,若规定成绩在80分以上(不含80分)为优秀,估计这次竞赛中成绩为优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的条件下,要使四边形ADCF为正方形,在△ABC中应添加什么条件,请直接把补充条件写在横线上 (不需说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com