
����Ŀ����ͼ����������ֽƬABCD�������²����� 
��i������D����һ��ֱ����BC���ཻ�ڵ�E1����ͼ�٣����ǡ�CDE1=��1��
��ii������ADE1��ƽ���߽�AB���ڵ�E2����ͼ�ڣ����ǡ�ADE2=��2��
��iii������CDE2��ƽ���߽�BC���ڵ�E3����ͼ�ۣ����ǡ�CDE3=��3��
���������Ӳ�����2�����ظ����ϲ��裬�õ���1 �� ��2 �� ������n �� �����������½��ۣ��ٵ���1=10��ʱ����2=40�㣻��2��4+��3=90�㣻 �۵���5=30��ʱ����CDE9�ա�ADE10���ܵ���1=45��ʱ��BE2= ![]() ��
��
������ȷ�ĸ���Ϊ�� ��
A.1
B.2
C.3
D.4
���𰸡�D
���������⣺�ٵ�a1=10��ʱ��a2= ![]() =40�㣬����ȷ�� ����ͼ�ۿ�֪��2a4+a3=90�㣬����ȷ��
=40�㣬����ȷ�� ����ͼ�ۿ�֪��2a4+a3=90�㣬����ȷ��
�۵�a5=30��ʱ��a9=30�㣬a10=30�㣬�ڡ�CDE9�͡�ADE10�У�
�� 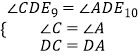 ��
��
���CDE9�ա�ADE10 �� ����ȷ��
�ܵ�a1=45��ʱ����E1���B�غϣ�
��E2F��BD��F��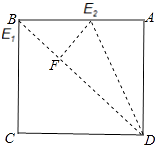
���ı���ABCD�������Σ�
���ABD=45�㣬
��BE2= ![]() FE2 ��
FE2 ��
��DE2ƽ�֡�ADB��E2F��BD����A=90�㣬
��AE2=FE2 ��
��BE2= ![]() AE2 �� ����ȷ��
AE2 �� ����ȷ��
��ѡ��D��
�����㾫�������������ε������ǽ����ĸ�������Ҫ֪���������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������Σ�


 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧϰС������ͬѧ����ĩģ�⿼�ԣ�����Ϊ120���ijɼ����£�100��100��x��x��80����֪�������ݵ���λ����ƽ������ȣ���ô����x��ֵ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪������y= ![]() x2+bx+c��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0����1����C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
x2+bx+c��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0����1����C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
��1����ͼ�����������߹�A��B���㣬��������ߵĺ�������ʽ��
��2��ƽ�ƣ�1���е������ߣ�ʹ����P��ֱ��AC�ϻ���������AC������һ��Q��
��i������M��ֱ��AC�·�����Ϊƽ��ǰ��1���е��������ϵĵ㣬����M��P��Q����Ϊ������������ǵ���ֱ��������ʱ��������з��������ĵ�M�����ꣻ
��ii��ȡBC���е�N������NP��BQ����̽�� ![]() �Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
�Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x+3�ֱ�x��y���ڵ�D��C����B��x���ϣ�OB=OC������B��ֱ��m��CD����P��Q�ֱ�Ϊֱ��m��ֱ��CD�ϵĶ��㣬�ҵ�P��x����Ϸ��������POQ=45��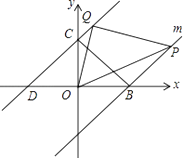
��1�����PBO=�ȣ�
��2���ʣ�PBCQ��ֵ�Ƿ�Ϊ��ֵ������ǣ�������ö�ֵ��������ǣ���˵�����ɣ�
��3����֤��CQ2+PB2=PQ2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������˶�Ա�������8�Σ����еĻ�����ͼ��ʾ�������л�������������λ���ֱ�Ϊ�� �� 
A.9����8��
B.8����9��
C.8����8.5��
D.8.5����9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ����֪��1=��2����3=��4����֤��AC��DF��BC��EF.֤���������£�
�ߡ�1=��2����֪����
��AC��DF��A��ͬλ����ȣ���ֱ��ƽ�У���
���3=��5��B���ڴ�����ȣ���ֱ��ƽ�У���
���ߡ�3=��4����֪��
���5=��4��C��������������
��BC��EF��D���ڴ�����ȣ���ֱ��ƽ�У���
�����������ж����ݴ�����ǣ� ��
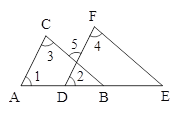
A. A B. B C. C D. D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���C=90�㣬BC=4cm��AC=3cm���ѡ�ABC�Ƶ�A˳ʱ����ת90��õ���A1B1C1����ͼ��ʾ�������߶�AB��ɨ�������Ϊ�� �� 
A.5 ![]()
B.![]() ��cm2
��cm2
C.![]() ��cm2
��cm2
D.5��cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
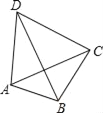
����Ŀ����ͼ���ı���ABCD�ĶԽ���AC��BD���ഹֱ����AB=3��BC=4��CD=5����AD�ij�Ϊ��������
A. 3![]() B. 4
B. 4![]() C. 2
C. 2![]() D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4���ף�����P�ӵ�A������AB����A��B��1����/����ٶ������ƶ�����P�����A��B�غϣ�������Q�ӵ�B�����ز���BC��CD��2����/����ٶ������ƶ�����P��Qͬʱ����������Pֹͣ�˶�����QҲ��ֹ֮ͣ������AQ��BD�ڵ�E�����P�˶�ʱ��Ϊt�롣
��1����t��ʾ�߶�PB�ij���
��2������Q���߶�BC���˶�ʱ��tΪ��ֵʱ����BEP�͡�BEQ��ȣ�
��3����tΪ��ֵʱ���߶�P��Q֮��ľ���Ϊ2![]() cm.
cm.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com