
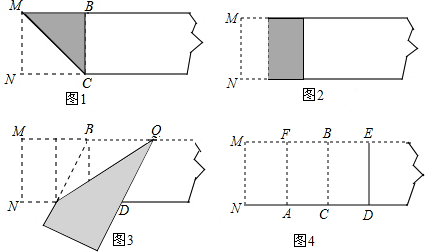
分析 (1)由折叠有BF=$\frac{1}{2}$BM=$\frac{1}{2}$MN=2,在Rt△ABF中,利用勾股定理计算即可;
(2)设正方形BCNM的边长为2a,利用对折的性质得AC=a,再在△ABC中根据勾股定理计算出AB=$\sqrt{5}$a,然后根据黄金矩形的定义进行判断.接着利用对折得AD=AB,所以CD=AD-AC即可;
(3)先判定四边形ADBQ是菱形,再用勾股定理计算即可.
解答 解:(1)由折叠有BF=$\frac{1}{2}$BM=$\frac{1}{2}$MN=2,
在Rt△ABF中,AF=MN=4,
∴AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=2$\sqrt{5}$,
故答案为2$\sqrt{5}$;
(2)设正方形BCNM的边长为2a,
∵正方形BCNM沿AF对折,
∴AC=$\frac{1}{2}$NC=a,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{5}$a,
∵AD=AB=$\sqrt{5}$a,
∴CD=AD-AC=($\sqrt{5}$-1)a,
∴$\frac{CD}{BC}$=$\frac{(\sqrt{5}-1)a}{2a}$=$\frac{\sqrt{5}-1}{2}$,
∴矩形BCDE就是黄金矩形,
故答案为BCDE.
(3)连接BD交AQ于点O,由折叠有∠BAQ=∠DAQ,AB=AD,
∴AQ⊥BD,BO=DO,
∵BQ∥AD,
∴∠DAQ=∠AQB,
∴∠BAQ=∠BQA,
∵AQ⊥BD,
∴OA=OQ,
∴四边形ADQB是平行四边形,
∵AB=AD,
∴四边形ADBQ是菱形,
∴AB=BQ=a,
根据勾股定理得,AB2=BF2+AF2,
∴a2=BF2+(2BF)2,
∴BF=$\frac{\sqrt{5}}{5}$a,
∴FQ=BF+BQ=$\frac{\sqrt{5}}{5}$a+a=(1+$\frac{\sqrt{5}}{5}$)a,AF=2BF=$\frac{2\sqrt{5}}{5}$a,
根据勾股定理得,AQ2=FQ2+AF2=[(1+$\frac{\sqrt{5}}{5}$)a]2+($\frac{2\sqrt{5}}{5}$a)2=2($\frac{1+\sqrt{5}}{5}$)a2,
∵AQ×BD=c,
∴BD=$\frac{c}{AQ}$,
∵AQ+BD=b,
∴AQ+$\frac{c}{AQ}$=b,
∴AQ2+$\frac{{c}^{2}}{A{Q}^{2}}$=b,
∴(AQ2)2+c2=bAQ2,
∴[2($\frac{1+\sqrt{5}}{5}$)a2]2+c2=b×2($\frac{1+\sqrt{5}}{5}$)a2
∴[2($\frac{1+\sqrt{5}}{5}$)a2-$\frac{b}{2}$]2=$\frac{{b}^{2}}{4}$-c2.
点评 此题几何变换综合题,主要考查了黄金分割,折叠的性质,勾股定理,解本题的关键是判定四边形ADBQ是菱形,找a,b,c的关系是本题的难点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
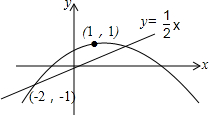 如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断:
如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10,26,24 | B. | 16,10,6 | C. | 30,17,8 | D. | 24,13,5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
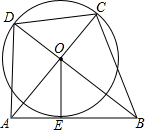 如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )
如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )| A. | 2+3$\sqrt{2}$ | B. | $\frac{3+2\sqrt{2}}{2}$ | C. | 4+2$\sqrt{2}$ | D. | 3+3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 85 | B. | 88 | C. | 95 | D. | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
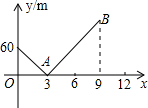 小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题:
小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com