
【题目】现有一次函数y=mx+n和二次函数y=mx2+nx+1,其中m≠0,
(1)若二次函数y=mx2+nx+1经过点(2,0),(3,1),试分别求出两个函数的解析式.
(2)若一次函数y=mx+n经过点(2,0),且图象经过第一、三象限.二次函数y=mx2+nx+1经过点(a,y1)和(a+1,y2),且y1>y2,请求出a的取值范围.
(3)若二次函数y=mx2+nx+1的顶点坐标为A(h,k)(h≠0),同时二次函数y=x2+x+1也经过A点,已知﹣1<h<1,请求出m的取值范围.
【答案】(1)y=x﹣2,y=![]() x2+
x2+![]() +1;(2)a<
+1;(2)a<![]() ;(3)m<﹣2或m>0.
;(3)m<﹣2或m>0.
【解析】
(1)直接将点代入函数解析式,用待定系数法即可求解函数解析式;
(2)点(2,0)代入一次函数解析式,得到n=2m,利用m与n的关系能求出二次函数对称轴x=1,由一次函数经过一、三象限可得m>0,确定二次函数开口向上,此时当 y1>y2,只需让a到对称轴的距离比a+1到对称轴的距离大即可求a的范围.
(3)将A(h,k)分别代入两个二次函数解析式,再结合对称抽得h=![]() ,将得到的三个关系联立即可得到
,将得到的三个关系联立即可得到![]() ,再由题中已知1<h<1,利用h的范围求出m的范围.
,再由题中已知1<h<1,利用h的范围求出m的范围.
(1)将点(2,0),(3,1),代入一次函数y=mx+n中,
![]() ,
,
解得![]() ,
,
∴一次函数的解析式是y=x﹣2,
再将点(2,0),(3,1),代入二次函数y=mx2+nx+1,
![]() ,
,
解得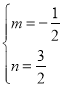 ,
,
∴二次函数的解析式是![]() .
.
(2)∵一次函数y=mx+n经过点(2,0),
∴n=﹣2m,
∵二次函数y=mx2+nx+1的对称轴是x=![]() ,
,
∴对称轴为x=1,
又∵一次函数y=mx+n图象经过第一、三象限,
∴m>0,
∵y1>y2,
∴1﹣a>1+a﹣1,
∴a<![]() .
.
(3)∵y=mx2+nx+1的顶点坐标为A(h,k),
∴k=mh2+nh+1,且h=![]() ,
,
又∵二次函数y=x2+x+1也经过A点,
∴k=h2+h+1,
∴mh2+nh+1=h2+h+1,
∴![]() ,
,
又∵﹣1<h<1,
∴m<﹣2或m>0.


科目:初中数学 来源: 题型:
【题目】已知,如图所示,在矩形ABCD中,点E在BC边上,△AEF=90°
(1)如图①,已知点F在CD边上,AD=AE=5,AB=4,求DF的长;
(2)如图②,已知AE=EF,G为AF的中点,试探究线段AB,BE,BG的数量关系;
(3)如图③,点E在矩形ABCD的BC边的延长线上,AE与BG相交于O点,其他条件与(2)保持不变,AD=5,AB=4,CE=1,求△AOG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
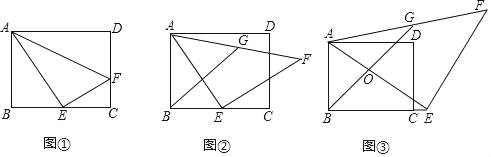
【题目】如图所示,在△ABD中,BC为AD边上的高线,tan∠BAD=1,在BC上截取CG=CD,连结AG,将△ACG绕点C旋转,使点G落在BD边上的F处,A落在E处,连结BE,若AD=4,tanD=3,则△CFD和△ECF的面积比为___;BE长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”
,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角” ![]() 约为
约为![]() ,而当手指接触键盘时,肘部形成的“手肘角”
,而当手指接触键盘时,肘部形成的“手肘角”![]() 约为
约为![]() .图
.图![]() 是其侧面简化示意图,其中视线
是其侧面简化示意图,其中视线![]() 水平,且与屏幕
水平,且与屏幕![]() 垂直.
垂直.

(![]() )若屏幕上下宽
)若屏幕上下宽![]() ,科学使用电脑时,求眼睛与屏幕的最短距离
,科学使用电脑时,求眼睛与屏幕的最短距离![]() 的长.
的长.
(![]() )若肩膀到水平地面的距离
)若肩膀到水平地面的距离![]() ,上臂
,上臂![]() ,下臂
,下臂![]() 水平放置在键盘上,其到地面的距离
水平放置在键盘上,其到地面的距离![]() ,请判断此时
,请判断此时![]() 是否符合科学要求的
是否符合科学要求的![]() ?
?
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
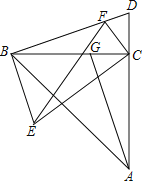
【题目】如图1,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.
(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,如图2,连接BE和CG. 求证:四边形BGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P(m,n)在抛物线y=ax2-4ax(a>0)上,E为抛物线的顶点.

(1)求点E的坐标(用含a的式子表示);
(2)若点P在第一象限,线段OP交抛物线的对称轴于点C,过抛物线的顶点E作x轴的平行线DE,过点P作x轴的垂线交DE于点D,连接CD,求证:CD∥OE;
(3)如图2,当a=1,且将图1中的抛物线向上平移3个单位,与x轴交于A、B两点,平移后的抛物线的顶点为Q,P是其x轴上方的对称轴上的动点,直线AP交抛物线于另一点D,分别过Q、D作x轴、y轴的平行线交于点E,且∠EPQ=2∠APQ,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com