
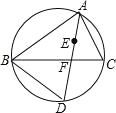
【题目】如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D.
(1)求证:∠BAD=∠CBD;
(2)求证:DE=DB.
科目:初中数学 来源: 题型:
【题目】某公司专销产品A,第一批产品A上市40天内全部售完、该公司对第一批产品A上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图(1)中的折线表示的是市场日销售量与上市时间的关系;图(2)中的折线表示的是每件产品A的销售利润与上市时间的关系.
(1)写出第一批产品A的市场日销售量y与上市时间t的关系式;
(2)写出每件产品A的销售利润y与上市时间t的关系式;
(3)第一批产品A上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=![]() +bx﹣
+bx﹣![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)b= ;点D的坐标: ;
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
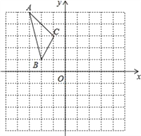
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛,对这两名运动员进行了10次测试,经过数据分析,甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024(s2),乙的方差为0.008(s2),则这10次测试成绩比较稳定的是运动员.(填“甲”或“乙”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com